A fair die is rolled. Let \(Y\) be the face value showing, 1, 2, 3, 4, 5, or 6 with each having the probability \(1 / 6\) of occurring. Let \(X\) be another random variable that is given by

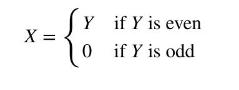
a. Find \(E(Y), E\left(Y^{2}\right)\), and \(\operatorname{var}(Y)\).

b. What is the probability distribution for \(X\) ? Find \(E(X), E\left(X^{2}\right)\), and \(\operatorname{var}(X)\).

c. Find the conditional probability distribution of \(Y\) given each \(X\).

d. Find the conditional expected value of \(Y\) given each value of \(X, E(Y \mid X)\).

e. Find the probability distribution of \(Z=X Y\). Show that \(E(Z)=E(X Y)=E\left(X^{2}\right)\).

f. Find \(\operatorname{cov}(X, Y)\).

Transcribed Image Text:

Y if Y is even X = 0 if Y is odd