A generalized version of the estimator for \(\beta_{2}\) proposed by Professor I.M. Mean for the regression model \(y_{i}=\beta_{1}+\beta_{2} x_{i}+e_{i}, i=1,2, \ldots, N\) is

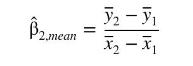
where \(\left(\bar{y}_{1}, \bar{x}_{1}\right)\) and \(\left(\bar{y}_{2}, \bar{x}_{2}\right)\) are the sample means for the first and second halves of the sample observations, respectively, after ordering the observations according to increasing values of \(x\). Given that assumptions MR1-MR6 hold:

a. Show that \(\hat{\beta}_{2, \text { mean }}\) is unbiased.

b. Derive an expression for \(\operatorname{var}\left(\hat{\beta}_{2, \text { mean }} \mid \mathbf{x}\right)\).

c. Write down an expression for \(\operatorname{var}\left(\hat{\beta}_{2, \text { mean }}\right)\).

d. Under what conditions will \(\hat{\beta}_{2, \text { mean }}\) be a consistent estimator for \(\beta_{2}\) ?

e. Randomly generate observations on \(x\) from a uniform distribution on the interval \((0,10)\) for sample sizes \(N=100,500,1000\), and, if your software permits, \(N=5000\). Assuming \(\sigma^{2}=1000\), for each sample size, compute:
i. \(\operatorname{var}\left(b_{2} \mid \mathbf{x}\right)\) and \(\operatorname{var}\left(\hat{\beta}_{2, \text { mean }} \mid \mathbf{x}\right)\) where \(b_{2}\) is the OLS estimator.
ii. Estimates for \(E\left[\left(s_{x}^{2}\right)^{-1}\right]\) and \(E\left[4 /\left(\bar{x}_{2}-\bar{x}_{1}\right)^{2}\right]\) where \(s_{x}^{2}\) is the sample standard deviation for \(x\) using \(N\) as a divisor.

f. Comment on the relative magnitudes of your answers in part (e), (i) and (ii) and how they change as sample size increases. Does it appear that \(\hat{\beta}_{2, \text { mean }}\) is consistent?

g. Show that \(E\left[\left(s_{x}^{2}\right)^{-1}\right] \xrightarrow{p} 0.12\) and \(E\left[4 /\left(\bar{x}_{2}-\bar{x}_{1}\right)^{2}\right] \xrightarrow{p} 0.16\). The variance of a uniform random variable defined on the interval \((a, b)\) is \((b-a)^{2} / 12\).

h. Suppose that the observations on \(x\) were not ordered according to increasing magnitude but were randomly assigned to any position. Would the estimator \(\hat{\beta}_{2, \text { mean }}\) be consistent? Why or why not?

Transcribed Image Text:

12.mean 2-1 X2X1