A life insurance company examines the relationship between the amount of life insurance held by a household

Question:

A life insurance company examines the relationship between the amount of life insurance held by a household and household income. Let INCOME be household income (thousands of dollars) and INSURANCE the amount of life insurance held (thousands of dollars). Using a random sample of $N=20$ households, the least squares estimated relationship is

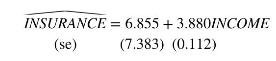
image text in transcribed

a. Draw a sketch of the fitted relationship identifying the estimated slope and intercept. The sample mean of $I N C O M E=59.3$. What is the sample mean of the amount of insurance held? Locate the point of the means in your sketch.

b. How much do we estimate that the average amount of insurance held changes with each additional $\$ 1000$ of household income? Provide both a point estimate and a $95 \%$ interval estimate. Explain the interval estimate to a group of stockholders in the insurance company.

c. Construct a $99 \%$ interval estimate of the expected amount of insurance held by a household with $\$ 100,000$ income. The estimated covariance between the intercept and slope coefficient is -0.746 .

d. One member of the management board claims that for every $\$ 1000$ increase in income the average amount of life insurance held will increase by $\$ 5000$. Let the algebraic model be INSURANCE $=$ $\beta_{1}+\beta_{2} I N C O M E+e$. Test the hypothesis that the statement is true against the alternative that it is not true. State the conjecture in terms of a null and alternative hypothesis about the model parameters. Use the 5\% level of significance. Do the data support the claim or not? Clearly, indicate the test statistic used and the rejection region.

e. Test the hypothesis that as income increases the amount of life insurance held increases by the same amount. That is, test the null hypothesis that the slope is one. Use as the alternative that the slope is larger than one. State the null and alternative hypotheses in terms of the model parameters. Carry out the test at the $1 \%$ level of significance. Clearly indicate the test statistic used, and the rejection region. What is your conclusion?