An author knows that a certain number of typographical errors \((0,1,2,3, \ldots)\) are on each book page. Define the random variable \(T\) equaling the number of errors per page. Suppose that \(T\) has a Poisson distribution [Appendix B.3.3], with \(p d

f, f(t)=\mu^{t} \exp (-\mu) / t\) !, where ! denotes the factorial operation, and \(\mu=E(T)\) is the mean number of typographical errors per page.

a. If \(\mu=3\), what is the probability that a page has one error? What is the probability that a page has four errors?

b. An editor independently checks each word of every page and catches \(90 \%\) of the errors, but misses \(10 \%\). Let \(Y\) denote the number of errors caught on a page. The values of \(y\) must be less than or equal to the actual number \(t\) of errors on the page. Suppose that the number of errors caught on a page with \(t\) errors has a binomial distribution

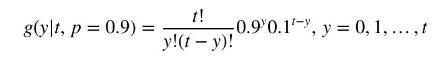
Compute the probability that the editor finds one error on a page given that the page actually has four errors.

c. Find the joint probability \(P[Y=3, T=4]\).

d. It can be shown that the probability the editor will find \(Y\) errors on a page follows a Poisson distribution with mean \(E(Y)=0.9 \mu\). Use this information to find the conditional probability that there are \(T=4\) errors on a page given that \(Y=3\) are found.

Transcribed Image Text:

t! g(ylt, p=0.9) = 0.90.1, y = 0, 1, ..., t y!(t-y)!