Consider a log-linear regression for the weekly sales of a national brand of canned tuna (brand \(A\) ), expressed as thousands of cans, CANS, as a function of the prices of two competing brands (brands \(B\) and \(C\) ), expressed as percentages of the price of brand \(A\). That is,

where \(R P R C E \_B=\left(P R I C E_{B} / P R I C E_{A}\right) \times 100\) and \(R P R C E_{-} C=\left(P R I C E_{C} / P R I C E_{A}\right) \times 100\).

a. Given assumptions MR1-MR5 hold, how do you interpret \(\beta_{2}\) and \(\beta_{3}\) ? What signs do you expect for these coefficients? Why?
Using \(N=52\) weekly observations, the least squares estimated equation is

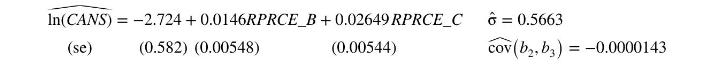
b. Using a \(10 \%\) significance level, test the null hypothesis that an increase in \(R P R C E \_B\) of one percentage point leads to a \(2.5 \%\) increase in the mean number of cans sold against the alternative that the increase is not \(2.5 \%\).

c. Using a \(10 \%\) significance level, test the null hypothesis that an increase in \(R P R C E \_C\) of one percentage point leads to a \(2.5 \%\) increase in the mean number of cans sold against the alternative that the increase is not \(2.5 \%\).

d. Using a \(10 \%\) significance level, test \(H_{0}: \beta_{2}=\beta_{3}\) against the alternative \(H_{1}: \beta_{2} eq \beta_{3}\). Does the outcome of this test contradict your findings from parts (b) and (c)?

e. Which brand do you think is the closer substitute for brand \(A\), brand \(B\), or brand \(C\) ? Why?

f. Use the corrected predictor introduced in Section 4.5.3 to estimate the expected number of brand \(A\) cans sold under the following scenarios:
i. \(R P R C E \_B=125, R P R C E_{-} C=100\)
ii. \(R P R C E_{-} B=111.11, R P R C E \_C=88.89\)
iii. \(R P R C E \_B=100, R P R C E \_C=80\)

g. The producers of brands \(B\) and \(C\) have set the prices of their cans of tuna to be \(\$ 1\) and 80 cents, respectively. The producer of brand \(A\) is considering three possible prices for her cans: 80 cents, 90 cents, or \(\$ 1\). Use the results from part

(f) to find which of these three price settings will maximize revenue from sales.

Transcribed Image Text:

In(CANS) = B + BRPRCE_B+B3RPRCE_C+ e