Consider the data file mroz on working wives and the model (ln (W A G E)=beta_{1}+beta_{2} E
Question:
Consider the data file mroz on working wives and the model \(\ln (W A G E)=\beta_{1}+\beta_{2} E D U C+\) \(\beta_{3} E X P E R+e\). Use the 428 observations on married women who participate in the labor force.
a. Write down in algebraic form the three moment conditions, like (10.13) and (10.14), that would lead to the OLS estimates of the model above.
b. Calculate the OLS estimates and residuals, \(\hat{e}_{i}\). What is the sum of the least squares residuals? What is the sum of squared least squares residuals? What is \(\sum E D U C_{i} \times \hat{e}_{i}\) ? What is \(\sum E X P E R_{i} \times \hat{e}_{i}\) ? Relate these results to the moment conditions in (a).
c. Calculate the fitted values \(\widehat{\ln (W A G E)}=b_{1}+b_{2} E D U C+b_{3} E X P E R\). What is the sample average of the fitted values? What is the sample average of \(\ln (W A G E), \overline{\ln (W A G E)}\) ?
d. Find each of the following:
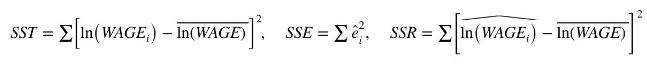
Compute \(S S R+S S E, R^{2}=S S R / S S T\) and \(R^{2}=1-S S E / S S T\). Explain what these calculations show about measuring goodness-of-fit.
Data From Equation 10.13 and 10.14:-
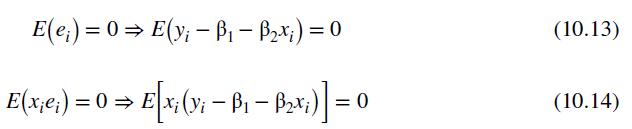
Step by Step Answer:

Principles Of Econometrics
ISBN: 9781118452271
5th Edition
Authors: R Carter Hill, William E Griffiths, Guay C Lim





