Consider the regression model (y_{i}=beta_{1}+beta_{2} x_{i}+e_{i}) where the pairs (left(y_{i}, x_{i} ight), i=1,2, ldots, N), are random

Consider the regression model \(y_{i}=\beta_{1}+\beta_{2} x_{i}+e_{i}\) where the pairs \(\left(y_{i}, x_{i}\right), i=1,2, \ldots, N\), are random independent draws from a population.

a. Suppose the marginal distribution of \(x_{i}\) is log-normal. To appreciate the nature of the log-normal distribution, consider a normal random variable \(W \sim N\left(\mu_{W}, \sigma_{W}^{2}\right)\). Then, \(X=e^{W}\) has a log-normal distribution with mean \(\mu_{X}=\exp \left(\mu_{W}+\sigma_{W}^{2} / 2\right)\) and variance \(\sigma_{X}^{2}=\left(\exp \left(\sigma_{W}^{2}\right)-1\right) \mu_{X}^{2}\). Assume that \(\left(e_{i} \mid x_{i}\right) \sim N\left(0, \sigma_{e}^{2}\right)\).

i. Will the least squares estimator \(\left(b_{1}, b_{2}\right)\) for the parameters \(\left(\beta_{1}, \beta_{2}\right)\) be unbiased?

ii. Will it be consistent?

iii. Will it be normally distributed conditional on \(\mathbf{x}=\left(x_{1}, x_{2}, \ldots, x_{N}\right)\) ?

iv. Will the marginal distribution of \(\left(b_{1}, b_{2}\right)\) (not conditional on \(\mathbf{x}\) ) be normally distributed?

v. Will \(t\)-tests for \(\beta_{1}\) and \(\beta_{2}\) be justified in finite samples or are they only large sample approximations?

vi. Suppose \(\mu_{w}=0, \sigma_{w}^{2}=1\), and \(x_{i}=\exp \left(w_{i}\right)\). What is the asymptotic variance of the least squares estimator for \(\beta_{2}\) ? (Express in terms of \(\sigma_{e}^{2}\) and \(N\).)

b. Suppose now that \(x_{i} \sim N(0,1)\) and that \(\left(e_{i} \mid x_{i}\right)\) has a log-normal distribution with mean and variance \(\mu_{e}=\exp \left(\mu_{v}+\sigma_{v}^{2} / 2\right)\) and \(\sigma_{e}^{2}=\left(\exp \left(\sigma_{v}^{2}\right)-1\right) \mu_{e}^{2}\), where \(v=\ln (e) \sim N\left(\mu_{v}, \sigma_{v}^{2}\right)\).

i. Show that we can rewrite the model as \(y_{i}=\beta_{1}^{*}+\beta_{2} x_{i}+e_{i}^{*}\) where

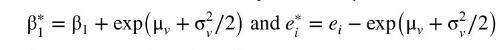
ii. Show that \(E\left(e_{i}^{*} \mid x_{i}\right)=0\) and \(\operatorname{var}\left(e_{i}^{*} \mid x_{i}\right)=\sigma_{e}^{2}\).
iii. Will the least squares estimator \(b_{2}\) for the parameter \(\beta_{2}\) be unbiased?
iv. Will it be consistent?
v. Will it be normally distributed conditional on \(\mathbf{x}=\left(x_{1}, x_{2}, \ldots, x_{N}\right)\) ?
vi. Will the marginal distribution of \(b_{2}\) (not conditional on \(\mathbf{x}\) ) be normally distributed?
vii. Will \(t\)-tests for \(\beta_{2}\) be justified in finite samples or are they only large sample approximations?
viii. What is the asymptotic variance of the least squares estimator for \(\beta_{2}\) ? (Express in terms of \(\sigma_{e}^{2}\) and \(N\).)

Transcribed Image Text:

B = B + exp(H, +/2) and e = e; - exp(, +/2)