Consider the simple regression model (y_{i}=beta_{1}+beta_{2} x_{i}+e_{i}) where we hypothesize heteroskedasticity of the form (sigma_{i}^{2}=sigma^{2} x_{i}^{2}). We
Question:
Consider the simple regression model \(y_{i}=\beta_{1}+\beta_{2} x_{i}+e_{i}\) where we hypothesize heteroskedasticity of the form \(\sigma_{i}^{2}=\sigma^{2} x_{i}^{2}\). We have \(N=4\) observations, with \(x=\left(\begin{array}{llll}1 & 2 & 3 & 4\end{array}\right)\) and \(y=\left(\begin{array}{llll}3 & 4 & 3 & 5\end{array}\right)\).
a. Use the formula for the least squares estimator in Exercise 8.2(b) to compute the OLS estimate of \(\beta_{2}\). In this case \(\sum x_{i 2} y_{i} / N=10, \quad \sum x_{i 2}^{2} / N=7\).
b. Referring to Exercise 8.2(c), what is the value \(c=\sum\left(1 / h_{i}\right)\) ?
c. Referring to Exercise 8.2(c), what are the values \(a_{i}=1 /\left(c h_{i}\right), i=1, \ldots, 4\) ? What is \(\sum_{i=1}^{4} a_{i}\) ?
d. Use the formula for the generalized least squares estimator in Exercise 8.2 (c) to compute the GLS estimate of \(\beta_{2}\).
e. Suppose that we know that \(\sigma^{2}=0.2\). Calculate the true OLS variance given in equation (8.8). The values of \(\left(x_{i}-\bar{x}\right)^{2}\) are \((2.25,0.25,0.25,2.25)\). What is the value of the incorrect variance in equation (8.6)?
Data From Exercise 8.2:-
Consider the regression model \(y_{i}=\beta_{1} x_{i 1}+\beta_{2} x_{i 2}+e_{i}\) with two explanatory variables, \(x_{i 1}\) and \(x_{i 2}\), but no constant term.
a. The sum of squares function is \(S\left(\beta_{1}, \beta_{2} \mid \mathbf{x}_{1}, \mathbf{x}_{2}\right)=\sum_{i=1}^{N}\left(y_{i}-\beta_{1} x_{i 1}-\beta_{2} x_{i 2}\right)^{2}\). Find the partial derivatives with respect to the parameters \(\beta_{1}\) and \(\beta_{2}\). Setting these derivatives to zero and solving and show that the least squares estimator of \(\beta_{2}\) is
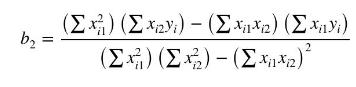
b. Let \(x_{i 1}=1\) and show that the estimator in (a) reduces to
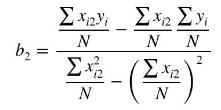
Compare this equation to equation (2A.5) and show that they are equivalent.
c. In the estimator in part (a), replace \(y_{i}, x_{i 1}\) and \(x_{i 2}\) by \(y_{i}^{*}=y_{i} / \sqrt{h_{i}}, x_{i 1}^{*}=x_{i 1} / \sqrt{h_{i}}\) and \(x_{i 2}^{*}=x_{i 2} / \sqrt{h_{i}}\). These are transformed variables for the heteroskedastic model \(\sigma_{i}^{2}=\sigma^{2} h\left(\mathbf{z}_{i}\right)=\sigma^{2} h_{i}\). Show that the resulting GLS estimator can be written as
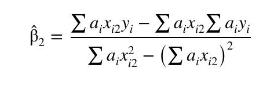
where \(a_{i}=1 /\left(c h_{i}\right)\) and \(c=\sum\left(1 / h_{i}\right)\). Find \(\sum_{i=1}^{N} a_{i}\).
d. Show that under homoskedasticity \(\hat{\beta}_{2}=b_{2}\).
e. Explain how \(\hat{\beta}_{2}\) can be said to be constructed from "weighted data averages" while the usual least squares estimator \(b_{2}\) is constructed from "arithmetic data averages." Relate your discussion to the difference between WLS and ordinary least squares.
Data From Equation 8.8 and 8.6:-
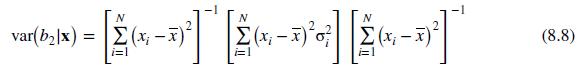
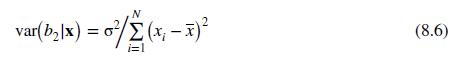
Data From Equation 2A.5:-
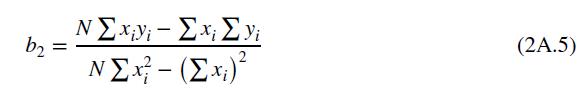
Step by Step Answer:

Principles Of Econometrics
ISBN: 9781118452271
5th Edition
Authors: R Carter Hill, William E Griffiths, Guay C Lim





