Consider the simplest version of equation (14.25). We have one dummy variable, x1i, and one other explanatory variable, x2i. Consequently, equation€(

14.25) reduces to

a) In this specification, demonstrate that δâ•›1 is the constant for the subpopulation with x1i = 0, μ1 is the effective constant for the subpopulation with x1i = 1, δâ•›2 is the coefficient on x2i for the subpopulation with x1i = 0, and μ2 is the coefficient on x2i for the subpopulation with x1i = 1.

(b) According to equation (14.8), the estimate of μ2 is

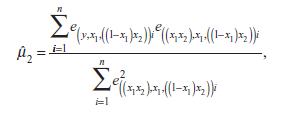
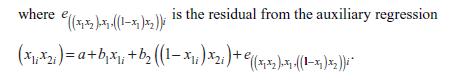
We won’t demonstrate it here, but the least squares estimates for this regression set a = bâ•›2 = 0. With these values, what are the predicted values of the dependent variable x1iâ•›x2i for the subpopulation with x1i = 0? What are the prediction errors?

(c) Based on the answer to part

b, what is the value of the product

from the numerator of the expression for μˆ2 for observations from the subpopulation with x1i = 0? What contribution do these observations make to the summation in that numerator?

(d) Based on the answer to part

c, what is the value of the square e x x x x x i 1 2 1 1 2 1 2 (( ), ,(( − ) )) from the denominator of the expression for μˆ2 for observations from the subpopulation with x1i = 0? What contribution do these observations make to the summation in that denominator?

(e) Based on the answers to parts c and

d, explain why observations from the subpopulation with x1i = 0 do not affect the calculation of μˆ2. Explain why the regression y x e i i i =μˆ +μˆ + , 1 2 2 applied only to the subpopulation with x1i = 1, would yield the same value for μˆ2 .

Transcribed Image Text:

y = (1-x)+8 (1-x) x2 +x +2x1, x2 +.