Designate the probability that a newborn child will be a girl as . The probability that a

Designate the probability that a newborn child will be a girl as π. The probability that a newborn child will be a boy is therefore 1 − π. Imagine that we have a sample that consists of a sequence of n births, beginning with girl, girl, boy, boy, boy, girl, boy, and so forth. Identify each birth with a subscript Â�giving the number of the birth in the sequence and a letter giving the sex of the child, g for girls and f for fellows, or boys. (We don’t want to use b for

“boy” because we’ve already used it so heavily.)

(a) We will need to assume that the sex for one birth is independent of the sex for any other birth. Does this seem reasonable? Why or why not?

(b) The probability of the observed sequence is P(sequence) = (gâ•›1 and gâ•›2 and fâ•›3 and fâ•›4 and fâ•›5 and gâ•›6 and fâ•›7 and . . .). Explain why this probability can be rewritten as

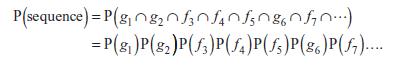
(c) Replace P(g) with π and P(╛╛f╛╛) with 1 − π wherever they appear in the Â�sequence. Imagine that, in total, m of the births were girls. Explain why the probability of the sequence can be rewritten as

(d) What is the natural logarithm of this probability?

(e) Replace the population probability π with p, its estimator. This expression is now the log-likelihood. Its derivative with respect to p is

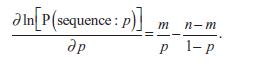
Set this derivative equal to zero and solve for p in terms of m and n.

(f) The second derivative of the log-likelihood with respect to p is

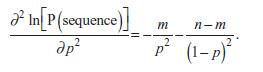
What is its value when p is equal to the estimator in part e? Does this value confirm that the estimator in part e maximizes the log-likelihood?
Why or why not?
(g) The value for p in part e is our MLE of π. Does it make intuitive sense?
Why or why not?

Transcribed Image Text:

P(sequence) = P(gf nn...) = P(g)P(g)P()P()P(s)P(g)P()....