For each of the following two time-series regression models, and assuming MR1-MR6 hold, find \(\operatorname{var}\left(b_{2} \mid \mathbf{x}\right)\) and examine whether the least squares estimator is consistent by checking whether \(\lim _{T \rightarrow \infty} \operatorname{var}\left(b_{2} \mid \mathbf{x}\right)=0\).

a. \(y_{t}=\beta_{1}+\beta_{2} t+e_{t}, t=1,2, \ldots, T\). Note that \(\mathbf{x}=(1,2, \ldots, T), \sum_{t=1}^{T}(t-\bar{t})^{2}=\sum_{t=1}^{T} t^{2}-\left(\sum_{t=1}^{T} t\right)^{2} / T\), \(\sum_{t=1}^{T} t=T(T+1) / 2\) and \(\sum_{t=1}^{T} t^{2}=T(T+1)(2 T+1) / 6\).

b. \(y_{t}=\beta_{1}+\beta_{2}(0.5)^{t}+e_{t}, t=1,2, \ldots, T\). Here, \(\mathbf{x}=\left(0.5,0.5^{2}, \ldots, 0.5^{T}\right)\). Note that the sum of a geometric progression with first term \(r\) and common ratio \(r\) is

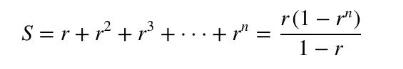
c. Provide an intuitive explanation for these results.

Transcribed Image Text:

S = r + r + r +...+ r(1-") 1-r