Recall the population expression for V(bIV) in equation (10.39): Complete the following derivation. Now that weve had
Question:
Recall the population expression for V(bIV) in equation (10.39):
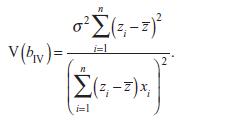
Complete the following derivation. Now that we’ve had nine chapters of practice at this sort of thing, we’re going to try it with a little less help than in previous exercises.
(a) Use the result of exercise 10.6a to rewrite the summation in the denominator as
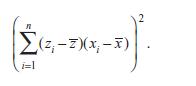
(b) Multiply both the numerator and the denominator by 1/(n − 1)2. Show that the numerator becomes σâ•›2V(zi)/(n − 1), where V(zi) represents the sample variance of zi. Show that the denominator becomes the square of the sample covariance between zi and xi, COV(zi, xi).
(c) With the replacements of part
b, show that
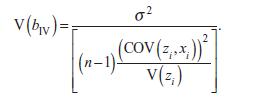
(d) Multiply the denominator by V(xi)/V(xi), where V(xi) represents the sample variance of xi. Demonstrate that
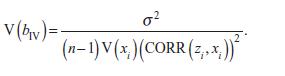
(e) Recall that all of the properties of bIV are asymptotic. Validate equation (10.43) by explaining why it’s acceptable to approximate the result of part€d with
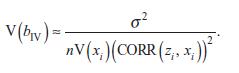
Step by Step Answer:







