Return to the calculation of the population value for SD(bIV) in table 10.5.

(a) In the context of measurement error, equation (10.5) defines the observed value of the explanatory variable, xi, as xi = xi* +νi .

In addition, we assumed that the measurement error, νi, is uncorrelated with the true value of the explanatory variable xi*. Explain why equation

(5.45) is valid for determining V(xi). Use it to establish that

Verify that V(xi) = 12.5 for table 10.5.

(b) For the purpose of simulation, we constructed our instrument, zi, for the regressions in table 10.5 using the following formula:

where ηi is a random variable with expected value zero and variance four, uncorrelated with xi* or νi. Explain why this is a valid instrument.
Confirm that

(c) This is the hard part, but we’ve already done a simpler version of it in exercise 10.2. The covariance between the observed explanatory variable and the instrument, COV(xi, zi), is

According to equation (5.8), this can be rewritten as

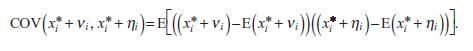
Explain why this can be rewritten, yet again, as

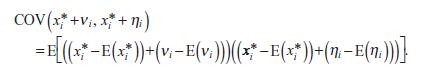
Expand to obtain

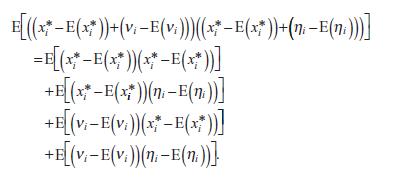
What rule of expectations justifies this expansion?

(d) Use equation (5.4) to demonstrate that the first term following the equality is V(xi*). Explain why the remaining three terms are all equal to zero.
Conclude that, in this case,

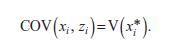
(e) Combine the results of parts

a, b,

c, and d to obtain

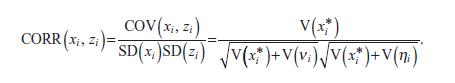
Verify that, with the values of the simulation for table 10.5, CORR(xi, zi)€= .6800.

Transcribed Image Text:

V(x)=V(x*)+V(vi).