Suppose we are able to collect a random sample of data on economics majors at a large university. Further suppose that, for those entering the workforce, we observe their employment status and salary 5 years after graduation. Let \(S A L=\$\) salary for those employed, \(G P A=\) grade point average on a 4.0 scale during their undergraduate program, with METRICS \(=1\) if student took econometrics, METRICS \(=0\) otherwise.

a. Consider the regression model \(S A L=\beta_{1}+\beta_{2} G P A+\beta_{3}\) METRICS \(+e\). Should we consider this a causal model, or a predictive model? Explain your reasoning.

b. Assuming \(\beta_{2}\) and \(\beta_{3}\) are positive, draw a sketch of \(E(S A L \mid G P A, M E T R I C S)=\beta_{1}+\beta_{2} G P A+\) \(\beta_{3}\) METRICS.

c. Define a dummy variable \(F E M A L E=1\), if the student is female; 0 otherwise. Modify the regression model to be \(S A L=\beta_{1}+\beta_{2} G P A+\beta_{3}\) METRICS \(+\delta_{1}\) FEMALE \(+e\). What is the expected salary of a male who has not taken econometrics? What is the expected salary of a female who has taken econometrics?

d. Consider the regression model

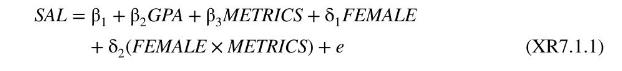
What is the expected salary of a male who has not taken econometrics? What is the expected salary of a female who has taken econometrics?

e. In the equation (XR7.1.1), assume that \(\delta_{1}

f. In equation (XR7.1.1), what are the null and alternative hypotheses, in terms of model parameters, for testing that econometrics training does not affect the average salary of economics majors? In order to use the test statistic in equation (6.4), what regression must you estimate in addition to (XR7.1.1)? What is the distribution of the test statistic if the null hypothesis is true assuming \(N=300\) ? What is the rejection region for a \(5 \%\) test?

Transcribed Image Text:

SAL = B+ BGPA + 3 METRICS +8, FEMALE +8(FEMALE X METRICS) + e (XR7.1.1)