The CAPM says that the risk premium on security \(j\) is related to the risk premium on the market portfolio. That is

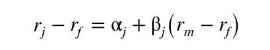
where \(r_{j}\) and \(r_{f}\) are the returns to security \(j\) and the risk-free rate, respectively, \(r_{m}\) is the return on the market portfolio, and \(\beta_{j}\) is the \(j\) th security's "beta" value. We measure the market portfolio using the Standard \& Poor's value weighted index, and the risk-free rate by the 30-day LIBOR monthly rate of return. As noted in Exercise 10.14, if the market return is measured with error, then we face an errors-in-variables, or measurement error, problem.

a. Use the observations on Microsoft in the data file capm5 to estimate the CAPM model using OLS. How would you classify the Microsoft stock over this period? Risky or relatively safe, relative to the market portfolio?

b. It has been suggested that it is possible to construct an IV by ranking the values of the explanatory variable and using the rank as the IV, that is, we sort \(\left(r_{m}-r_{f}\right)\) from smallest to largest, and assign the values \(R A N K=1,2, \ldots, 180\). Does this variable potentially satisfy the conditions IV1-IV3? Create RANK and obtain the first-stage regression results. Is the coefficient of RANK very significant? What is the \(R^{2}\) of the first-stage regression? Can RANK be regarded as a strong IV?

c. Compute the first-stage residuals, \(\hat{v}\), and add them to the CAPM model. Estimate the resulting augmented equation by OLS and test the significance of \(\hat{v}\) at the \(1 \%\) level of significance. Can we conclude that the market return is exogenous?

d. Use RANK as an IV and estimate the CAPM model by IV/2SLS. Compare this IV estimate to the OLS estimate in part (a). Does the IV estimate agree with your expectations?

e. Create a new variable \(P O S=1\) if the market return \(\left(r_{m}-r_{f}\right)\) is positive, and zero otherwise. Obtain the first-stage regression results using both RANK and POS as instrumental variables. Test the joint significance of the IV. Can we conclude that we have adequately strong IV? What is the \(R^{2}\) of the first-stage regression?

f. Carry out the Hausman test for endogeneity using the residuals from the first-stage equation in (e). Can we conclude that the market return is exogenous at the \(1 \%\) level of significance?
g. Obtain the IV/2SLS estimates of the CAPM model using RANK and POS as instrumental variables. Compare this IV estimate to the OLS estimate in part (a). Does the IV estimate agree with your expectations?
h. Obtain the IV/2SLS residuals from part (g) and use them (not an automatic command) to carry out a Sargan test for the validity of the surplus IV at the 5\% level of significance.

Data From Exercise 10.14:-

The Capital Asset Pricing Model (CAPM) says that the risk premium on security \(j\) is related to the risk premium on the market portfolio, that is

where \(r_{j}\) and \(r_{f}\) are the returns to security \(j\) and the risk-free rate, respectively, \(r_{m}\) is the return on the market portfolio, and \(\beta_{j}\) is the \(j\) th security's "beta" value. A stock's beta is important to investors since it reveals the stock's volatility. We measure the market portfolio using the Standard \& Poors value weighted index, and the risk-free rate by the 30-day LIBOR monthly rate of return.

a. Using 180 monthly observations from January 1988, the OLS estimate of IBM's beta is 0.9769 with a standard error of 0.0978 . If our constructed values of the market return and the risk-free rate are measured with error is the OLS estimator unbiased and consistent? If it is biased, what is the direction of the bias?

b. It has been suggested that it is possible to construct an IV by ranking the values of the explanatory variable and using the rank as the IV. That is, we sort \(\left(r_{m}-r_{f}\right)\) from smallest to largest, and assign the values \(R A N K=1,2, \ldots, 180\). Does this variable potentially satisfy the conditions IV1-IV3?

c. The estimated first-stage regression of \(\left(r_{I B M}-r_{f}\right)\) on \(R A N K\) yields an overall \(F\)-test of model significance of 93.77. What can we conclude about the strength of the IV RANK?

d. If we compute the first-stage residuals and add them to the CAPM model, the resulting coefficient has a \(t\)-value of 60.60. What does this result suggest to us about the OLS estimator in the CAPM model?

e. Using RANK as an IV and estimating the CAPM model by IV/2SLS yield an estimate of IBM's beta of 1.0025 with a standard error of 0.1019 . Compare this IV estimate to the OLS estimate in part (a). Does the IV estimate agree with your expectations?

Transcribed Image Text:

r; -r;=; + ; (rm-r)