The data file liquor contains observations on annual expenditure on liquor (LIQUOR) and annual income (INCOME) (both
Question:
The data file liquor contains observations on annual expenditure on liquor (LIQUOR) and annual income (INCOME) (both in thousands of dollars) for 40 randomly selected households for three consecutive years.
a. Create the first-differenced observations on LIQUOR and INCOME. Call these new variables LIQUORD and INCOMED. Using OLS regress LIQUORD on INCOMED without a constant term. Construct a \(95 \%\) interval estimate of the coefficient.
b. Estimate the model LIQUOR \(_{i t}=\beta_{1}+\beta_{2} I N C O M E_{i t}+u_{i}+e_{i t}\) using random effects. Construct a \(95 \%\) interval estimate of the coefficient on INCOME. How does it compare to the interval in part (a)?
c. Test for the presence of random effects using the LM statistic in equation (15.35). Use the 5\% level of significance.
d. For each individual, compute the time averages for the variable INCOME. Call this variable INCOMEM. Estimate the model LIQUOR \(_{i t}=\beta_{1}+\beta_{2}\) INCOME \(_{i t}+\gamma\) INCOMEM \(_{i}+c_{i}+e_{i t}\) using the random effects estimator. Test the significance of the coefficient \(\gamma\) at the \(5 \%\) level. Based on this test, what can we conclude about the correlation between the random effect \(u_{i}\) and INCOME? Is it OK to use the random effects estimator for the model in (b)?
Data From Equation 15.35:-
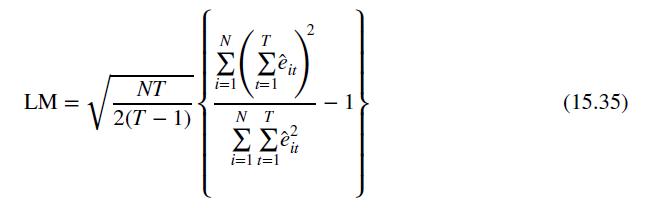
Step by Step Answer:

Principles Of Econometrics
ISBN: 9781118452271
5th Edition
Authors: R Carter Hill, William E Griffiths, Guay C Lim





