The discussion of equation (10.7) asserts that i is uncorrelated with xi because it is uncorrelated with

The discussion of equation (10.7) asserts that εi is uncorrelated with xi because it is uncorrelated with xi* and νi. Let’s prove that here.

(a) Explain why the population covariance between two random variables must be zero if they are uncorrelated.

(b) Prove that COV(εi, xi* + νi) = COV(εi, xi*) + COV(εi, νi). Begin by invoking equation (5.8):

Rearrange to obtain

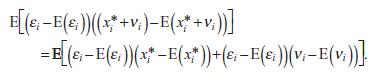
Demonstrate that the term to the left of the equality is equal to COV(εi, xi*) + COV(εi, νi).

(c) Our assumptions regarding equation (10.4) assert that COV(εi, xi*) = 0.
Our assumptions regarding νi assert that COV(εi, νi) = 0. Use these assumptions and the result of part b to prove that COV(εi, xi) = 0.

Transcribed Image Text:

COV (,, x*+v;)=E[(&-E(&;))((x* +v;) E(x* +v;))]-