This question is designed to clarify some of the results used to explain HAC standard errors.

a. Given that \(\widehat{\operatorname{var}}\left(\hat{q}_{t}\right)=(T-2)^{-1} \sum_{t=1}^{T}\left(x_{t}-\bar{x}\right)^{2} \hat{e}_{t}^{2}\) and \(s_{x}^{2}=T^{-1} \sum_{t=1}^{T}\left(x_{t}-\bar{x}\right)^{2}\), show that

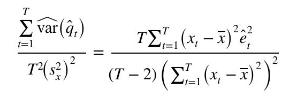
b. For \(T=4\), write out all the terms in the summations

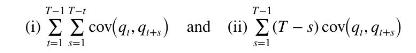
What assumption is necessary for these two summations to be equal?

c. For the simple regression model \(y_{t}=\alpha+\beta_{0} x_{t}+e_{t}\) with \(E\left(e_{t} \mid x_{t}\right)=0\) show that \(\operatorname{cov}\left(e_{t}, e_{s} \mid x_{t}, x_{s}\right)=0\) for \(t eq s\) implies \(\operatorname{cov}\left(q_{t}, q_{s}\right)=0\) where \(q_{t}=\left(x_{t}-\mu_{x}\right) e_{t}\).

Transcribed Image Text:

T var var (.) ( - ) 2.2