Using data on 1000 home loan borrowers, we estimate the linear probability model

where \(D E F A U L T=1\) if the borrower has made a mortgage payment more than 90 days late, \(L T V=100\) (loan amount/property value), RATE is the interest rate, AMOUNT ( \(\$ 10,000\) units) of the loan, and FICO is the borrower's credit score.

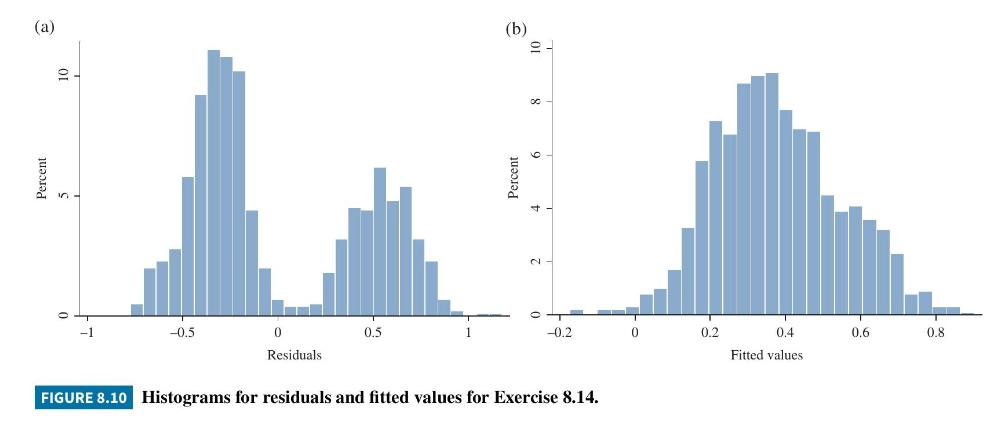
a. Figure 8.10 (a) is the histogram of the least squares residuals, \(\hat{e}\). Explain the bimodal shape.

b. Figure 8.10 (b) is the histogram of the least squares fitted values,

Explain the interpretation of the fitted values. Do you find any unusual fitted values in the figure?

c. Let \(Y\) be a Bernoulli random variable, taking the values 1 and 0 with probabilities \(P\) and \(1-P\). Show that \(\operatorname{var}(Y)=P(1-P)\).

d. Regressing \(\hat{e}_{i}^{2}\) on the explanatory variables, we obtain \(R^{2}=0.0206\) and the model \(F\)-statistic is 5.22. What does each of these values tell us about the null hypothesis of homoskedasticity in this model? Provide any relevant test statistics, and their \(5 \%\) level of significance critical values. In light of part (c), are the results surprising?

e. Consider two hypothetical borrowers:
Borrower 1: \(L T V=85, R A T E=11, A M O U N T=400, F I C O=500\)
Borrower 2: \(L T V=50, R A T E=5, A M O U N T=100, F I C O=700\)

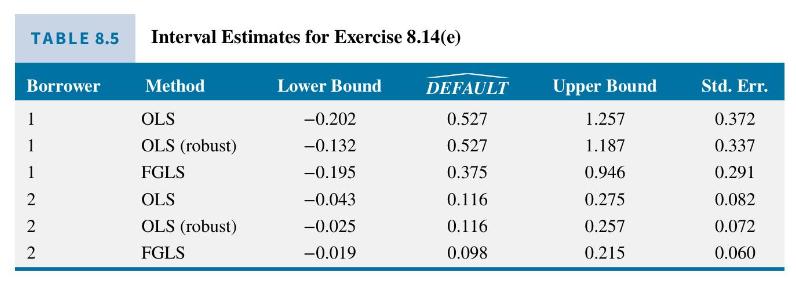
The 95\% interval estimates, for the expected probability of default for the hypothetical borrowers using OLS, OLS with heteroskedasticity robust standard errors, and FGLS are given in Table 8.5. Discuss these interval estimates. If two such borrowers came for a loan, to whom would you offer one?

f. To obtain the FGLS estimates in (e), negative predicted values in nine observations are turned to positives by taking their absolute value. Why did we do that? What other alternatives did we have?

Transcribed Image Text:

DEFAULT = B + BLTV+ BRATE + BAMOUNT + FICO + e