Using the “cluster” option in the econometrics package Stata® 11, the fully robust standard errors for the pooled OLS estimates in Table 14.2—that is, robust to serial correlation and heteroskedasticity in the composite errors,

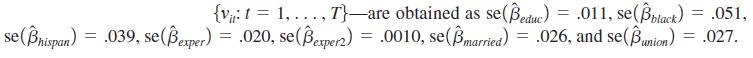
(i) How do these standard errors generally compare with the nonrobust ones, and why?

(ii) How do the robust standard errors for pooled OLS compare with the standard errors for RE? Does it seem to matter whether the explanatory variable is time-constant or time-varying?

(iii) When the fully robust standard errors for the RE estimates are computed, Stata® 11 reports the following (where we look at only the coefficients on the time-varying variables):

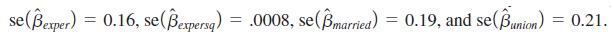
[These are robust to any kind of serial correlation or heteroskedasticity in the idiosyncratic errors {u_it: t = 1, . . . . , T} as well as heteroskedasticity in α_i.] How do the robust standard errors generally compare with the usual RE standard errors reported in Table 14.2? What conclusion might you draw?

(iv) Comparing the four standard errors in part (iii) with their pooled OLS counterparts, what do you make of the fact that the robust RE standard errors are all below the robust pooled OLS standard errors?

Transcribed Image Text:

{V4: t = 1, ..., T}-are obtained as se(Beduc) = .011, se(Bolack) .0010, se(Bmarriea) se(Bnispan) = .039, se(Berper) = .020, se(Beper2) = .026, and se(Bunion) = .027.