Based on Exhibit 2, which portfolio provides the greatest objective function expected value?

A. Portfolio 1 B. Portfolio 2 C. Portfolio 3 Megan Beade and Hanna Müller are senior analysts for a large, multi-divisional money management firm. Beade supports the institutional portfolio managers, and Müller does the same for the private wealth portfolio managers.

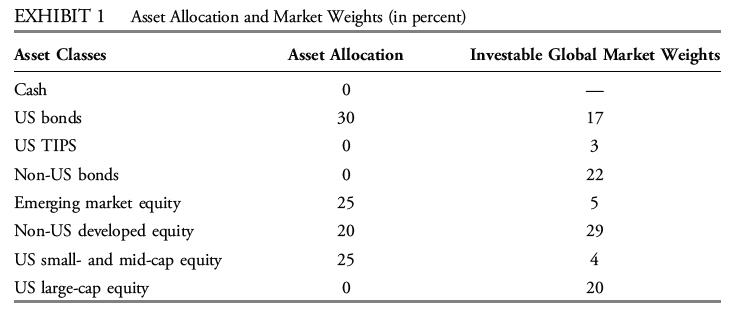
Beade reviews the asset allocation in Exhibit 1, derived from a mean–variance optimization (MVO) model for an institutional client, noting that details of the MVO are lacking.
The firm’s policy is to rebalance a portfolio when the asset class weight falls outside of a corridor around the target allocation. The width of each corridor is customized for each client and proportional to the target allocation. Beade recommends wider corridor widths for highrisk asset classes, narrower corridor widths for less liquid asset classes, and narrower corridor widths for taxable clients with high capital gains tax rates.
One client sponsors a defined benefit pension plan where the present value of the liabilities is $241 million and the market value of plan assets is $205 million. Beade expects interest rates to rise and both the present value of plan liabilities and the market value of plan assets to decrease by $25 million, changing the pension plan’s funding ratio.
Beade uses a surplus optimization approach to liability-relative asset allocation based on the objective function

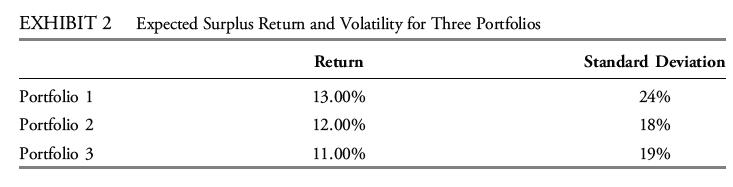
where E(Rs,m) is the expected surplus return for portfolio m, λ is the risk aversion coefficient, and σ²(Rs,m) is the variance of the surplus return. Beade establishes the expected surplus return and surplus variance for three different asset allocations, shown in Exhibit 2. Given λ ¼ 1.50, she chooses the optimal asset mix.
Client Haunani Kealoha has a large fixed obligation due in 10 years. Beade assesses that Kealoha has substantially more funds than are required to meet the fixed obligation.

The client wants to earn a competitive risk-adjusted rate of return while maintaining a high level of certainty that there will be sufficient assets to meet the fixed obligation.
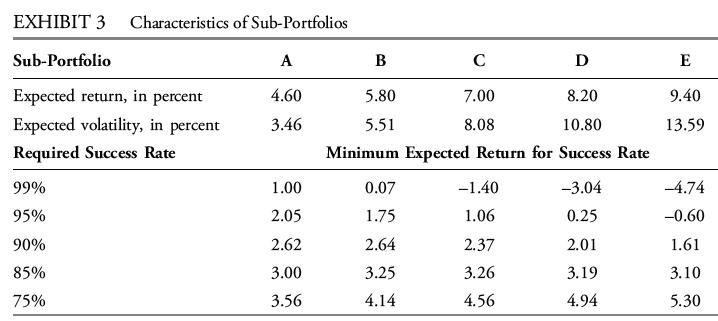
In the private wealth area, the firm has designed five sub-portfolios with differing asset allocations that are used to fund different client goals over a five-year horizon. Exhibit 3 shows the expected returns and volatilities of the sub-portfolios and the probabilities that the sub-portfolios will exceed an expected minimum return. Client Luis Rodríguez wants to satisfy two goals. Goal 1 requires a conservative portfolio providing the highest possible minimum return that will be met at least 95% of the time. Goal 2 requires a riskier portfolio that provides the highest minimum return that will be exceeded at least 85% of the time.
Müller uses a risk parity asset allocation approach with a client’s four–asset class portfolio. The expected return of the domestic bond asset class is the lowest of the asset classes, and the returns of the domestic bond asset class have the lowest covariance with other asset class returns. Müller estimates the weight that should be placed on domestic bonds.
Müller and a client discuss other approaches to asset allocation that are not based on optimization models or goals-based models. Müller makes the following comments to the client:
Comment 1: An advantage of the “120 minus your age” heuristic over the 60/40 stock/
bond heuristic is that it incorporates an age-based stock/bond allocation.
Comment 2: The Yale model emphasizes traditional investments and a commitment to active management.
Comment 3: A client’s asset allocation using the 1/N rule depends on the investment characteristics of each asset class.

Transcribed Image Text:

EXHIBIT 1 Asset Allocation and Market Weights (in percent) Asset Classes Cash US bonds US TIPS Non-US bonds Asset Allocation 0 Investable Global Market Weights 17 73252 30 0 0 Emerging market equity 25 Non-US developed equity 20 29 US small- and mid-cap equity 25 4 US large-cap equity 0 20