The difference in meaning of the arithmetic and geometric mean, holding Extell stock over the period January 1, 2008, through December 31, 2012, for two different investment strategies, is as follows: 

Strategy A—keep a fixed amount (say, $1,000) invested and do not reinvest returns. Strategy B—reinvest returns and allow compounding. 

First, take Extell’s returns and convert them to decimal form (r) for Strategy A and then to (1 + r) form for Strategy B.

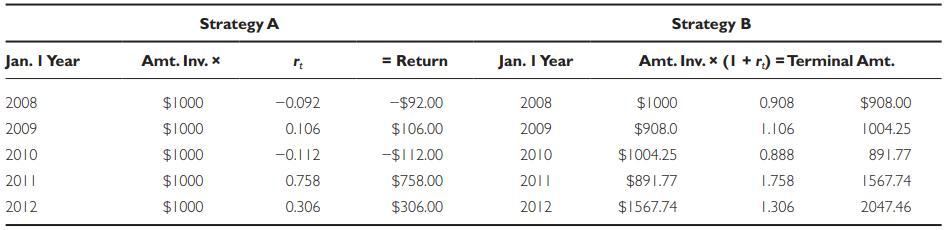
Using Strategy A, keeping $1,000 invested at the beginning of the year, total returns for the years 2008–2012 were $966, or $193.20 per year average ($966/5), which on a $1,000 investment is $193.20 ÷ 1,000 = 0.1932, or 19.32 percent per year—the same value as the arithmetic mean in Demonstration. Using Strategy B, compounding gains and losses, total return was $1,047.46 (the terminal amount $2,047.46 minus the initial $1,000). The average annual rate of return in this situation can be found by taking the nth root of the terminal/initial amount:

which is exactly the set of values we ended up with in Demonstration when calculating the geometric mean.

Transcribed Image Text:

Jan. I Year 2008 2009 2010 2011 2012 Strategy A Amt. Inv. x $1000 $1000 $1000 $1000 $1000 -0.092 0.106 -0.112 0.758 0.306 = Return -$92.00 $106.00 -$112.00 $758.00 $306.00 Jan. I Year 2008 2009 2010 2011 2012 Strategy B Amt. Inv. x (1 + r) = Terminal Amt. $1000 $908.0 $1004.25 $891.77 $1567.74 0.908 1.106 0.888 1.758 1.306 $908.00 1004.25 891.77 1567.74 2047.46