Imagine a candy bar that has k places where it can be cut. You would like to know how many different sequences of cuts are possible to divide the bar into pieces. For example, if k is 3, you could cut the bar at location 1, then location 2, and finally at location 3. We indicate this sequence of cuts by 123. So if k is 3, we have six ways to divide the bar: 123, 132, 213, 231, 312, or 321. Notice that we have k possibilities for making the first cut. Once we make the first cut we have k − 1 places where a cut must be made. Recursively, this can be expressed as

C(k) = kC(k − 1)

Let’s make this a bit more interesting by adding a restriction. You must always cut the leftmost pieces that can be cut. Now if k is 3, we can cut the bar at locations 123, 132, 213, 312, or 321. A cutting sequence of 231 would not be allowed, because after the cut at 2 we would have to make the cut at location 1, since it is the leftmost piece. We still have k possibilities for making the first cut, but now we have to count the number of ways to cut two pieces and multiply. Recursively, this can be expressed as

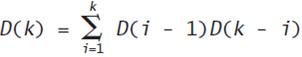
When k is 3, we would compute

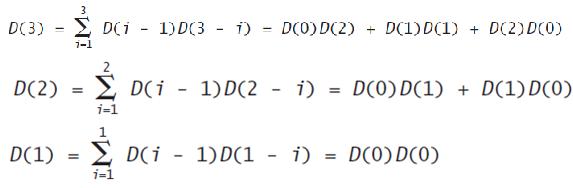
For both recursive formulas, if k 5 0, there is exactly one way to divide the bar.
Develop a program that will read a value of k from the keyboard and then display C(k)and D(k). (D(k) is interesting because it turns out to be the number of ways that we can parenthesize an arithmetic expression that has k binary operators.)

k D(k) 2 D(i - 1)D(k - i) i=1