Repeat Exercise 12 in Chapter 7, but use an instance of ArrayList instead of an array. Make the following slight changes to the methods to reflect that an ArrayList object can grow in size:

• Change the constructor’s parameter from the maximum degree to the desired degree.
• The method setConstant might need to add zero-valued coefficients before a. For example, if a = 3, a = 5, a = 0, a = 2, a = 0, and a = 0, the polynomial would be of degree 3, since the last nonzero constant is a . The invocation setConstant(8, 15) would need to set a and a to 0 and a to 15.

Exercise 12 in Chapter 7

Create a class Polynomial that is used to evaluate a polynomial function of x:

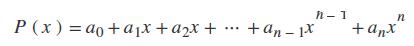
The coefficients a are floating-point numbers, the exponents of x are integers, and the largest exponent n—called the degree of the polynomial—is greater than or equal to 0. The class has the attributes

• degree—the value of the largest exponent n
  coefficients—an array of the coefficients a 

and the following methods:

• Polynomial(max)—a constructor that creates a polynomial of degree max whose coefficients are all 0
• setConstant(i, value)—sets the coefficient a to value
• evaluate(x)—returns the value of the polynomial for the given value x

For example, the polynomial

P (x) = 3 + 5x + 2x³

is of degree 3 and has coefficients a₀ = 3, a₁ = 5, a₂ = 0, and a₃ = 2. The invocation evaluate(7) computes 3 + 5 × 7 + 0 × 7 + 2 = 7₃, which is 3 + 35 + 0 + 686, and returns the result 724.

P (x) = ao+ax +a2x + ** +an 1X +anx