In part (c) of Exercise 6.22, we developed a solution to the Knight’s Tour problem. The approach used, called the “accessibility heuristic,” generates many solutions and executes efficiently.

As computers continue to increase in power, we’ll be able to solve more problems with sheer computer power and relatively unsophisticated algorithms. Let’s call this approach “brute-force” problem solving.

a) Use random-number generation to enable the knight to walk around the chessboard (in its legitimate L-shaped moves) at random. Your application should run one tour and display the final chessboard. How far did the knight get?

b) Most likely, the application in part (a) produced a relatively short tour. Now modify your application to attempt 1,000 tours. Use a one-dimensional array to keep track of the number of tours of each length. When your application finishes attempting the 1,000 tours, it should display this information in neat tabular format. What was the best result?

c) Most likely, the application in part (b) gave you some “respectable” tours, but no full tours. Now let your application run until it produces a full tour. Once again, keep a table of the number of tours of each length, and display this table when the first full tour is found. How many tours did your application attempt before producing a full tour? How much time did it take?

d) Compare the brute-force version of the Knight’s Tour with the accessibility-heuristic version. Which required a more careful study of the problem? Which algorithm was more difficult to develop? Which required more computer power? Could we be certain (in advance) of obtaining a full tour with the accessibility-heuristic approach? Could we be certain (in advance) of obtaining a full tour with the brute-force approach? Argue the pros and cons of brute-force problem solving in general.

Exercise 6.22(c)

After attempting to write and run a Knight’s Tour application, you’ve probably developed some valuable insights. We’ll use these insights to develop a heuristic (i.e., a common-sense rule) for moving the knight. Heuristics do not guarantee success, but a carefully developed heuristic greatly improves the chance of success. You may have observed that the outer squares are more troublesome than the squares nearer the center of the board. In fact, the most troublesome or inaccessible squares are the four corners. Intuition may suggest that you should attempt to move the knight to the most troublesome squares first and leave open those that are easiest to get to, so that when the board gets congested near the end of the tour, there will be a greater chance of success. We could develop an “accessibility heuristic” by classifying each of the squares according to how accessible it is and always moving the knight (using the knight’s Lshaped moves) to the most inaccessible square. We label a two-dimensional array accessibility with numbers indicating from how many squares each particular square is accessible. On a blank chessboard, each of the 16 squares nearest the center is rated as 8, each corner square is rated as 2, and the other squares have accessibility numbers of 3, 4 or 6 as follows:

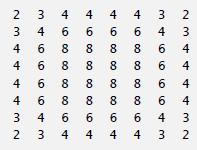
Write a new version of the Knight’s Tour, using the accessibility heuristic. The knight should always move to the square with the lowest accessibility number. In case of a tie, the knight may move to any of the tied squares. Therefore, the tour may begin in any of the four corners. As the knight moves around the chessboard, your application should reduce the accessibility numbers as more squares become occupied. In this way, at any given time during the tour, each available square’s accessibility number will remain equal to precisely the number of squares from which that square may be reached.] Run this version of your application. Did you get a full tour? Modify the application to run 64 tours, one starting from each square of the chessboard. How many full tours did you get?

Transcribed Image Text:

NM + + + + 3 N Waar oor w +0 00 00 00 00 0 00 00 00 00 +60 00 00 00 00 4 m 3 +666643 432 4 4 234