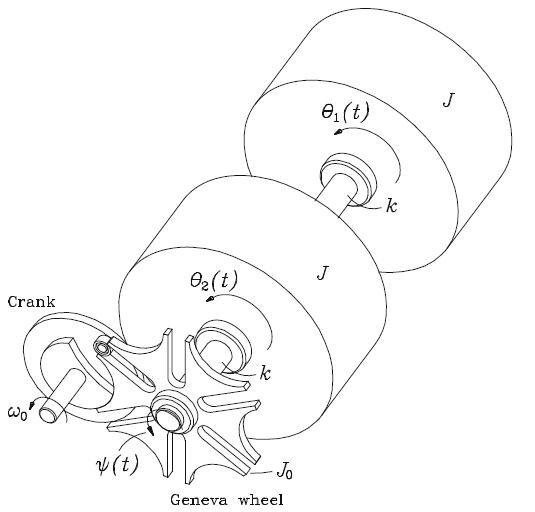
We analyzehere the model of the driving mechanism of the mechanism shown in Fig. 4.13, for p

We analyzehere the model of the driving mechanism of the mechanism shown in Fig. 4.13, forψ_p(t) given as

Figure 4.13

and displayed in Fig. 5.27, while f (t) is given, in turn, as

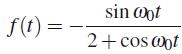
Figure 5.27

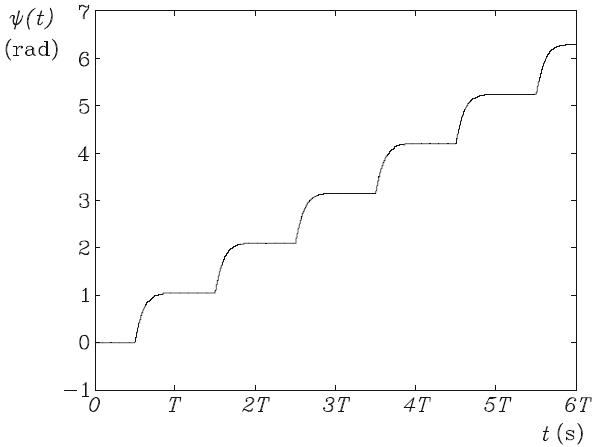
(a) Compute the coefficients of the first N_h harmonic components of the foregoing periodic function, by dividing the period in 2N_h intervals of equal length. Produce a table of error e in the Fourier approximation of ψ_p(t) vs. N_h, forN_h = 1, 2, 3, 4, 5, 10, and 20. Comment on your tabulated results. 

(b) Find the steady-state response of the system, i.e., θ₁(t) and θ₂(t), for Nh harmonics of the Fourier expansion of ψ_p(t). Choose the smallest value of N_h that will give you an error smaller than 0.05 in the approximation of ψ_p(t). Plot θ₁(t) and θ₂(t) vs. time in the [0, 4T] interval. Note that these plots are composed of a periodic and a nonperiodic part.

For the calculation, use the numerical values

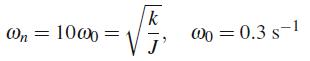
(c) In order to design the two shafts of the mechanism, we need the root-mean square value of the torque experienced by each shaft, which you are asked to provide. Find also the maximum absolute values of these torques.

Transcribed Image Text:

Wp(t) = = 37, 3 (t - T) + arctan[f(t)], for 0