A B-spline is built out of B-spline segments, described in Exercise 2. Let p_{0,................,}p₄ be control points. For 0 ≤ t ≤ 1, let x(t) and y(t) be determined by the geometry matrices [p₀ p₁ p₂ p₃] and [p₁ p₂ p₃ p₄], respectively. Notice how the two segments share three control points. The two segments do not overlap, however—they join at a common endpoint, close to p₂.
a. Show that the combined curve has G0 continuity—that is, x(1) = y(0).
b. Show that the curve has C¹ continuity at the join point, x(1). That is, show that x'(1) = y'(0).

Data From Exercise 2

The parametric vector form of a B-spline curve was defined in the Practice Problems as

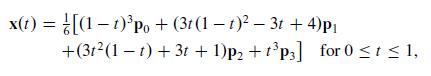
where p₀, p₁, p₂, and p₃ are the control points.

Transcribed Image Text:

x(t) = [(1-1)³ Po + (31 (1-1)² - 3t+4)P₁ +(3t²(1 t) + 3t+1)p2 +1³p3] for 0 ≤ t ≤ 1,