Given A = QR as in Theorem 12, describe how to find an orthogonal m m

Question:

Given A = QR as in Theorem 12, describe how to find an orthogonal m × m (square) matrix Q₁ and an invertible n × n upper triangular matrix R such that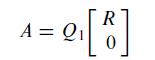

The MATLAB qr command supplies this "full" QR factorization when rank A = n.

Data from in Theorem 12

Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Related Book For book-img-for-question

Linear Algebra And Its Applications

ISBN: 9781292351216

6th Global Edition

Authors: David Lay, Steven Lay, Judi McDonald

See More Books

Question Posted: May 15, 2023 06:31 AM

In this exercise we consider how to generate matrices with specified ranks using MATLAB. (a) In general, if A is an m n matrix with rank r, then r min(m, n). Why? Explain. If the entries of A are...
Concern the (real) Schur factorization of an n x n matrix A in the form A = URU T , where U is an orthogonal matrix and R is an n x n upper triangular matrix. 1 a. Let A be an n x n diagonalizable...
In this problem, we shall outline a Bayesian solution to the problem described in Example 7.5.10 on page 423. Let = 1/ 2 and use a proper normal-gamma prior of the form described in Sec. 8.6. In...
The labor force participation rate is increasing in Japan because... a) there are fewer unemployed people b) the working age population is increasing c) retirement ages are increasing d) more women...
Find the following values by using the Poisson tables in Appendix A. a. P (x = 6 | = 3.8) b. P (x > 7 | = 2.9) c. P (3 x 9 | = 4.2) d. P (x = 0 | = 1.9) e. P (x 6 | = 2.9) f. P (5 < x 8 | =...
For the cash flows in the previous problem, what is the NPV at a discount rate of 0%? What if the discount rate is 10%? If it is 20%? If it is 30%? Data in previous problem, What is the IRR of the...
The Pitot tube on a supersonic aircraft (see Video V3.8) cruising at an altitude of $30,000 \mathrm{ft}$ senses a stagnation pressure of 12 psia. If the atmosphere is considered standard, determine...
Karges Coffee Inc. manufactures a line of single-cup brewing machines for home and office use that brew a cup of coffee, tea, or hot chocolate in less than a minute. The machines use specially...
The average molecular velocity v of a gas in a certain container is given by o(T) = 30T m/s, where T is the temperature in kelvins. The temperature is related to the pressure (in atmospheres) by T =...
Suppose A = QR is a QR factorization of an m n matrix A (with linearly independent columns). Partition A as [A 1 A 2 ], where A 1 has p columns. Show how to obtain a QR factorization of A 1 , and...
Let A be an m x n matrix such that the matrix A T A is invertible. Let x 1 and x 2 be the least squares solutions of equations Ax = b 1 and Ax = b 2 respectively. Show that c 1 x 1 + c 2 x 2 is the...
To discourage people from signing up at the Promise Cash Center site discussed in Exercise 3, write an online article. Imagine that youll post your article on a site that warns consumers about...
Rank these atoms by the number of electrons they tend to lose, from fewest to most: (a) sodium, Na; (b) magnesium, Mg; (c) aluminum, Al.
Why does it make sense to think that the alcohol is made of very tiny particles (molecules) rather than being an infinitely continuous material?
Generally, what types of changes in desired saving and desired investment lead to large current account deficits in a small open economy? What factors lead to these changes in desired saving and...
Why does it take so much more energy to boil 10 grams of liquid water than to melt 10 grams of ice?
Rank these noble-gas atoms by their number of filled shells, from least to most: (a) argon, (b) radon, (c) helium, (d) neon.
What are the reasons why an FI may choose to hedge selectively its portfolio?
Differentiate. y = ln(3x + 1) ln(5x + 1)
Conduct a simulation analysis with 1000 shuffles. Indicate how to determine the approximate p-value from the simulation results and report that p-value.
Use the 2SD rule to generate a 95% confidence interval on the long-run difference in means between the two groups.
Interpret the 95% confidence interval you obtained in #10.
A coding supervisor performs an internal audit on the coding staff. The overall accuracy results are 85 percent and the expectation is 95 percent. She decides to eliminate the worst records from the...
Prior to working for ABC Co., DJ worked for one of ABC Co.'s service providers for 3 years and spent all three of those years providing services to ABC Co. DJ joined ABC Co. as an employee 5 years...
create journal entries 1) On December 5, ACME purchased $56,250 of merchandise on account from Indiana Corp terms 2/10, n/30. Date Account description Debit Credit

Given A = QR as in Theorem 12, describe how to find an orthogonal m m

Question:

4= 0₁ [8] A Q

Step by Step Answer:

1To find an orthogonal m m matrix Q1 and an invertible n n upper triangular matrix R such that A QR ...View the full answer

Linear Algebra And Its Applications

Students also viewed these Mathematics questions