Suppose the transfer function W(s) in Exercise 21 is invertible for some s. It can be shown

Question:

Suppose the transfer function W(s) in Exercise 21 is invertible for some s. It can be shown that the inverse transfer function W (s)^-1, which transforms outputs into inputs, is the
Schur complement of A - BC - sI_n for the matrix below. Find this Schur complement. See Exercise 17.

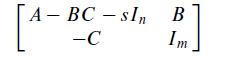
Data from in Exercise 21

Assume A - SI_n is invertible and view (8) as a system of two matrix equations. Solve the top equation for x and substitute into the bottom equation. The result is an equation of the form W(s)u = y, where W(s) is a matrix that depends on s. W(s) is called the transfer function of the system because it transforms the input u into the output y. Find W(s) and describe how it is related to the partitioned system matrix on the left side of (8).

Data from in Exercise 17

Suppose A₁₁ is invertible. Find X and Y such that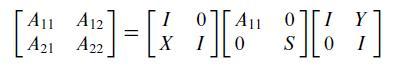

where S = A₂₂ - A₂₁A^-¹₁₁A₁₂. The matrix S is called the Schur complement of A₁₁. Likewise, if A₂₂ is invertible, the matrix A₁₁ - A₁₂ 4^-1₂₂ 4₂₁ is called the Schur complement of A₂₂. Such expressions occur frequently in the theory of systems engineering, and elsewhere.