Verify the Cayley-Hamilton Theorem for A =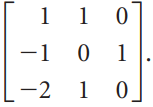

The Cayley-Hamilton Theorem can be used to calculate powers and inverses of matrices. For example, if A is a 2 × 2 matrix with characteristic polynomial c_A(λ) = λ² + aλ + b, then A² + aA + bI = O, so 

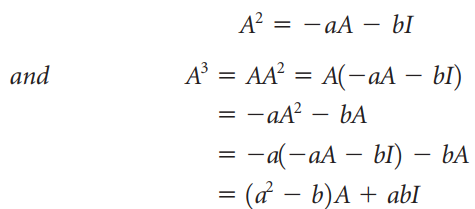
It is easy to see that by continuing in this fashion we can express any positive power of A as a linear combination of I and A. From A² + aA + bI = O, we also obtain A(A + aI ) = -bI, so

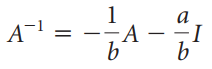
provided b ‰  0.

Transcribed Image Text:

-1 -2 0. A? = - aA – bI A = AA? = A(-aA – bl) = -aA? – bA and — -а(-аА — ы) — bА bl) – bA (a – b)A + abI I|||