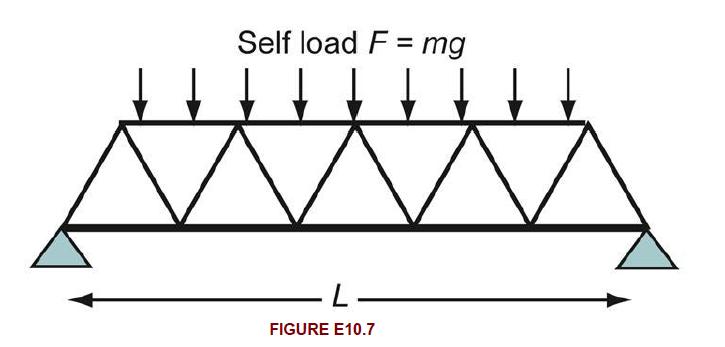
Question: A steel truss bridge shown in Fig. E10.7 has a span (L) and is simply supported at both ends. It weighs (m) tonnes. As a
A steel truss bridge shown in Fig. E10.7 has a span \(L\) and is simply supported at both ends. It weighs \(m\) tonnes. As a rule of thumb, bridges are designed with a stiffness \(S_{B}\) such that the central deflection \(\delta\) of a span under its self-weight is less than \(1 / 300\) of the length \(L\) (thus \(S_{B} \geq 300 \mathrm{mg} / L\) where \(g\) is the acceleration due to gravity, \(9.81 \mathrm{~m} / \mathrm{s}^{2}\) ). Use this information to calculate a minimum value for the shape factor \(\phi_{B}^{e}\) of the three steel truss bridge spans listed in the table. Take the density \(ho\) of steel to be \(7900 \mathrm{~kg} / \mathrm{m}^{3}\) and its modulus \(E\) to be \(205 \mathrm{GPa}\). The constant \(C_{1}=384 / 5=76.8\) for uniformly distributed load (Appendix B, Section B3).

Bridge Engineering Handbook, 2nd edition, (2014), W-F Chen and L. Duan (Eds), CRC Press, London.
Data From Fig, E10.7
Bridge and Construction Date Span L (m) Mass m (tonnes) 132 Royal Albert bridge, Tamar, Saltash UK (1857) 139 Carquinez Strait bridge, California (1927) Chesapeake Bay bridge, Maryland USA (1952) 146 1060 650 850
Step by Step Solution
3.40 Rating (156 Votes )
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


