Let’s see whether quadratic voting can avoid the paradox of voting that arose in Table 5.3 when using 1p1v in a series of pairedchoice majority votes. To reexamine this situation using quadratic voting, the following table presents the maximum willingness to pay of Garcia, Johnson, and Lee for each of the three public goods. Notice that each person’s numbers for willingness to pay match her or his ordering of preferences (1st choice, 2nd choice, 3rd choice) presented in Table 5.3. Thus, Garcia is willing to spend more on her 1st choice of national defense ($400)

than on her second choice of a road ($100) or her third choice of a weather warning system ($0).

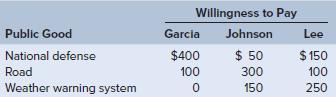
a. Assume that voting will be done using a quadratic voting system and that Garcia, Johnson, and Lee are each given $500 that can only be spent on purchasing votes (i.e., any unspent money has to be returned). How many votes will Garcia purchase to support national defense? How many for the road?
Place those values into the appropriate blanks in the table below and then do the same for the blanks for Johnson and Lee.

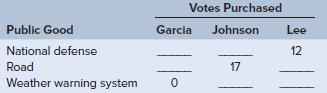
b. Across all three voters, how many votes are there in favor of national defense? The road? The weather warning system?

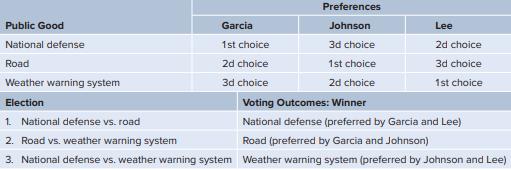
c. If a paired-choice vote is taken of national defense versus the road, which one wins?

d. If a paired-choice vote is taken of the road versus the weather warning system, which one wins?

e. If a paired-choice vote is taken of national defense versus the weather warning system, which one wins?

f. Review your answers to parts

c, d, and

e. Has quadratic voting eliminated the paradox of voting that we found when using 1p1v?

Table 5.3:

Transcribed Image Text:

Public Good National defense Road Weather warning system Willingness to Pay Johnson $ 50 300 150 Garcia $400 100 0 Lee $150 100 250