This exercise requires you to compute inflationary expectations based on a simple formula, and it will help you to understand why backward-looking expectations adjust slowly to changes in economic events. Suppose that the actual inflation rate in year \(t\) is denoted \(\Pi_{t}\). Expected inflation for year \(t+1\) is denoted \(\mathrm{II}_{t+1}^{e}\). Now, suppose that workers and firms form their expectations according to

where \(\Pi^{T}\) is the central bank's announced inflation target. This simple equation says that people's expectations for inflation at \(t+1\) are a weighted average of last year's actual inflation rate and the central bank's currently announced target. We will use this equation to see how the size of \(\theta\) determines the extent to which expectations are backward-looking. Consider the table below, which shows the data for a reduction in actual inflation from 10 percent to 2 percent.

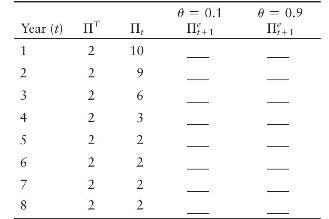
a. Assume that \(\theta\) is equal to 0 .1 . Compute expected inflation for each year and fill in the table.

b. On a scale diagram, plot the time path of actual inflation, expected inflation, and the inflation target.

c. Now assume that \(\theta\) equals 0 .9 . Repeat parts

(a) and (b).

d. Which value of \(\theta\) corresponds to more backwardlooking expectations? Explain.

e. Given the different speed of adjustment of inflationary expectations, predict which disinflation is more costly in terms of lost output-the one with \(\theta=0.1\) or with \(\theta=0.9\). Explain.

Transcribed Image Text:

11+1=11(10), (with 0 < < < 1)