Colway Company estimates the relation between the demand for its products and the price it sets, in

Question:

Colway Company estimates the relation between the demand for its products and the price it sets, in terms of this equation where:

\[
\begin{aligned}
& Q=\text { the quantity demanded } \\
& P=\text { the price of the product } \\
& Q=a-b P
\end{aligned}
\]

The marketing manager, Trisha Colway, conducted a market research study last fall that indicated that $b=500$ and $a=8,400$ on average for the first quarter of this year.
Capacity costs are $m=\$ 3$ per unit, and variable costs are $v=\$ 8.10$ per unit. If committed capacity is exceeded, the variable costs increase to $w=\$ 12.70$ per unit.
Trisha determined that the long-term benchmark price is given by the following:

\[
\begin{aligned}
P^{L} & =\frac{a}{2 b}+\frac{v+m}{2} \\
& =\frac{8,400}{2 \times 500}+\frac{\$ 8.10+\$ 3.00}{2} \\
& =\$ 13.95
\end{aligned}
\]

Trisha also set the capacity level at $X=2,150$ units.
Colway Company keeps track of demand conditions throughout the quarter. It announces a new price for each week in the Sunday newspaper based on the most current information it has on demand conditions. The following are the estimates of the demand parameter for each of the 13 weeks in the first quarter of this year:

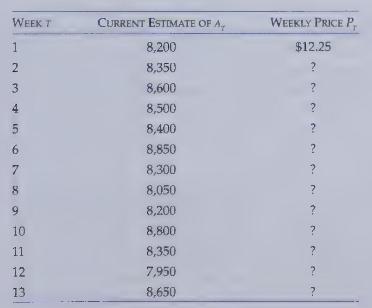
image text in transcribed

The estimate of $b$ remained at $b=500$ for all 13 weeks. The short-term (weekly) price is set at this if the capacity is not exceeded by the realized demand:
\[ P_{t}^{*}=\frac{a_{t}}{2 b}+\frac{v}{2} \]
It is set at this if the capacity is exceeded:
\[ P_{t}^{*}=\frac{a_{t}}{2 b}+\frac{w}{2} \]
Note that if the price is set at this:
\[ P_{t}^{*}=\frac{a_{t}}{2 b}+\frac{v}{2} \]
the resultant demand will not exceed the capacity $X=2,150$ only if this occurs:
\[ Q_{t}=a_{t}-b P_{t}=a_{t}-500\left(\frac{a_{t}}{1,000}+\frac{8.10}{2}\right)=\frac{a_{t}}{2}-2,025 \]
is less than $X=2,150$, that is, if $a_{t} \leq 8,350$. Similarly, if the price is set at this;
\[ P_{i}^{*}=\frac{a_{t}}{2 b}+\frac{w}{2} \]
the resultant demand will exceed the capacity $X=2,150$ only if $a_{t}>10,650$.
Required

a. Determine the weekly prices, plot them on a graph for each of the 13 weeks, and compare them with the long-term benchmark price. What is the average of the weekly prices?

b. Determine the total profit over the 13-week period. Repeat the same exercise after setting the capacity (X) at different levels (X = 1,750, 1,950, 2,350, and 2,550). Plot the total profit on a graph against different levels of capacity that you select.