optimaI eontraet Ralph owns a production funetion. Randomness in the environment pius Iabor input from a manager eombine to produce output. The output can be one of two quantities: Xl < x2• The manager's input can be one of two quantities, L < H. Ralph is risk neutraI. The probabilities are given below: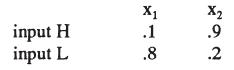

Assume the higher output is sufficiently attractive that Ralph wants supply of input H in all that follows.
Ralph's manager is risk averse and also ineurs an unobservable personal eost in supplying the labor input. We model this in the usual way. The manager' s utility for wealth w is given by U(w) = -exp{-r'W). It the manager suppHes input aE{H,L}, thereby incurring personal eost ca' and is paid amount I, wealth will total I - el' We use CH = 5,000 and cL = 0, along with a risk aversion parameter of r = .0001. Also, the manager's opportunity eost of working for Ralph is U(M), with M = 10,000.
a] Suppose the manager is trustworthy and will honor any agreement (or, equivalentIy, serious penalties are feasible and the manager' s input can be observed.)
What is the eost to Ralph of aequiring input H?

b] Suppose the only obselVable for eontraeting purposes is the manager' s output.
Determine the optimal pay-for-performance arrangement.2S What is the eost to Ralph of aequiring input H? Draw the manager's decision tree and verify the manager ean do no better than accept Ralph's terms and then supply input H. What is the manager' s eertain equivalent for the payment lottery that is faced?
e] Why, in your solution to part [b] above, is the manager paid more when the largest feasible output (i.e., x:z) is obselVed?AppendixLO1