square root utility Ralph owns a produetion function that uses labor input to produce output.

Outputwill be eitherxI = 10,000 orx2 = 20,000. Laboris supplied by an agent. One of three possible supplies wiIl be used: H > B > L. The output probabilities are displayed below: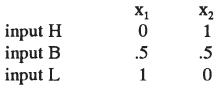

Ralph is risk neutraI. The agent has a utility funetion for payment z and labor supply a of U(z,a) = v'z - Vea), with V(H) = 60, V(B) = 30, and V(L) = 5. In addition, the agent's next best offer earries a pay, labor supply paekage that provides an expeeted utility of 40. So whatever Ralph dreams up, the expeeted value of U(z,a) must be at least 40 if the agent is to be attraeted.

a] Ralph must decide which aE{L,B,H} to acquire, and how to compensate the agent for this supply of labor. If the agent can be trusted to supply whatever is agreed upon, it is straightfOIward to figure out C

(a) = [40 + V(a)]7. Determine C(a)
for each aE{L,B,H}. What is Ralph's best choice?
b] Now assume output is the only contracting variable. Determine the best compensation package to motivate supp ly of (i) a = L, (ii) a = B, and (iii) a = H. In turn, what is Ralph's best choice and why does this differ from the best choice in the case where the agent can be trusted?
e] In the a = B case immediately above, you should have found the agent is paid more if the high output is produced. Why is this the case?AppendixLO1

Transcribed Image Text:

input H input B input L 205- .5 150 .5 1 0