Suppose instead of (14.16) on page 294, we had chosen the scheme where the last term in
Question:
Suppose instead of (14.16) on page 294, we had chosen the scheme
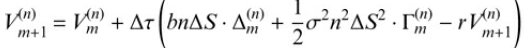
where the last term in parenthesis is with respect to time τ = (m + 1)Δτ. Prove that this scheme is still explicit and use a martingale argument to show that the stability condition (14.23) on page 295, as well as the additional condition σ2n≥ b have to hold, in order for the scheme to be consistent.
(14.16)
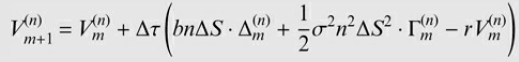
(14.23)
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





