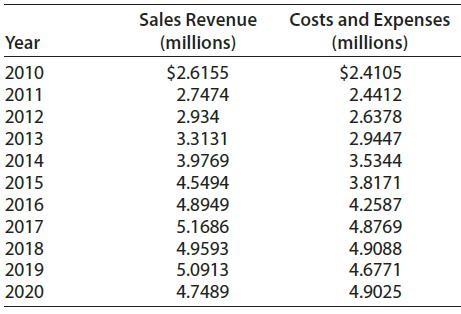
Assume that costs and expenses for Continental Divide Mining can be modeled by

C(t) = - 0.012t² + 0.492t + 0.725

where t is the number of years past 2007.

(a) Use R(t) as given in Problem 20 and form the profit function (as a function of time).

(b) Use the function from (a) to find the year in which maximum profit occurs.

(c) Graph the profit function from (a) and the data points from the table.

(d) Through the decade from 2015 to 2025, does the function project increasing or decreasing profits? Do the data support this trend (as far as it goes)?

The data in the table give sales revenues and costs and expenses for Continental Divide Mining for various years.

Transcribed Image Text:

Sales Revenue Costs and Expenses (millions) Year (millions) 2010 $2.6155 $2.4105 2011 2.7474 2.4412 2012 2.934 2.6378 2013 3.3131 2.9447 2014 3.9769 3.5344 2015 4.5494 3.8171 2016 4.8949 4.2587 2017 5.1686 4.8769 2018 4.9593 4.9088 2019 5.0913 4.6771 2020 4.7489 4.9025