Consider the problem of forced oscillations.

a. Derive the general solution in Equation (2.77).

b. Plot the solutions in Equation (2.77) for the following cases: Let \(c_{1}=0.5, c_{2}=0, F_{0}=1.0 \mathrm{~N}\), and \(m=1.0 \mathrm{~kg}\) for \(t \in[0,100]\).

i. \(\omega_{0}=2.0 \mathrm{rad} / \mathrm{s}, \omega=0.1 \mathrm{rad} / \mathrm{s}\).

ii. \(\omega_{0}=2.0 \mathrm{rad} / \mathrm{s}, \omega=0.5 \mathrm{rad} / \mathrm{s}\).

iii. \(\omega_{0}=2.0 \mathrm{rad} / \mathrm{s}, \omega=1.5 \mathrm{rad} / \mathrm{s}\).

iv. \(\omega_{0}=2.0 \mathrm{rad} / \mathrm{s}, \omega=2.2 \mathrm{rad} / \mathrm{s}\).

v. \(\omega_{0}=1.0 \mathrm{rad} / \mathrm{s}, \omega=1.2 \mathrm{rad} / \mathrm{s}\).

vi. \(\omega_{0}=1.5 \mathrm{rad} / \mathrm{s}, \omega=1.5 \mathrm{rad} / \mathrm{s}\).

c. Derive the form in Equation (2.78).

d. Confirm that the solution in Equation (2.78) is the same as the solution in Equation (2.77) for \(F_{0}=2.0 \mathrm{~N}, m=10.0 \mathrm{~kg}, \omega_{0}=\) \(1.5 \mathrm{rad} / \mathrm{s}\), and \(\omega=1.25 \mathrm{rad} / \mathrm{s}\), by plotting both solutions for \(t \in\) \([0,100]\).

Data from Equation 2.77

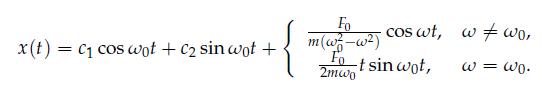
Data from Equation 2.78

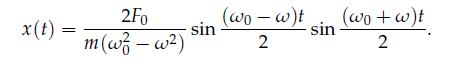
x(t) = C cos wot + C sin wot + Fo m(w-w) cos wt, wwo, Fo 2mwo t sin wot, = Wo