In this problem you will derive the expansion [x^{2}=frac{c^{2}}{2}+4 sum_{j=2}^{infty} frac{J_{0}left(alpha_{j} x ight)}{alpha_{j}^{2} J_{0}left(alpha_{j} c ight)}, quad 0 where the (alpha_{j}{ }^{prime} s) are the

In this problem you will derive the expansion

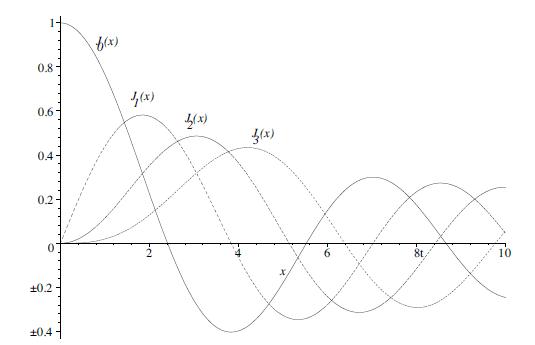
\[x^{2}=\frac{c^{2}}{2}+4 \sum_{j=2}^{\infty} \frac{J_{0}\left(\alpha_{j} x\right)}{\alpha_{j}^{2} J_{0}\left(\alpha_{j} c\right)}, \quad 0

where the \(\alpha_{j}{ }^{\prime} s\) are the positive roots of \(J_{1}(\alpha c)=0\), by following the below steps.

a. List the first five values of \(\alpha\) for \(J_{1}(\alpha c)=0\) using Table 6. 3 and Figure 6. 8. [Be careful in determining \(\alpha_{1}\).]

b. Show that \(\left\|J_{0}\left(\alpha_{1} x\right)\right\|^{2}=\frac{c^{2}}{2}\). Recall that \[\left\|J_{0}\left(\alpha_{j} x\right)\right\|^{2}=\int_{0}^{c} x J_{0}^{2}\left(\alpha_{j} x\right) d x\]

c. Show that \(\left\|J_{0}\left(\alpha_{j} x\right)\right\|^{2}=\frac{c^{2}}{2}\left[J_{0}\left(\alpha_{j} c\right)\right]^{2}, j=2,3, \ldots\). (This is the most involved step.) First note from Problem 18 that \(y(x)=\) \(J_{0}\left(\alpha_{j} x\right)\) is a solution of \[x^{2} y^{\prime \prime}+x y^{\prime}+\alpha_{j}^{2} x^{2} y=0\]
i. Verify the Sturm-Liouville form of this differential equation: \(\left(x y^{\prime}\right)^{\prime}=-\alpha_{j}^{2} x y\)
ii. Multiply the equation in part i. by \(y(x)\) and integrate from \(x=0\) to \(x=c\) to obtain \[\begin{align*} \int_{0}^{c}\left(x y^{\prime}\right)^{\prime} y d x & =-\alpha_{j}^{2} \int_{0}^{c} x y^{2} d x \\ & =-\alpha_{j}^{2} \int_{0}^{c} x J_{0}^{2}\left(\alpha_{j} x\right) d x \tag{6.172} \end{align*}\]
iii. Noting that \(y(x)=J_{0}\left(\alpha_{j} x\right)\), integrate the left-hand side by parts and use the following to simplify the resulting equation: 1. \(J_{0}^{\prime}(x)=-J_{1}(x)\) from Equation (6.6o). 2. Equation \((6.63)\) 3. \(J_{2}\left(\alpha_{j} c\right)+J_{0}\left(\alpha_{j} c\right)=0\) from Equation (6.61).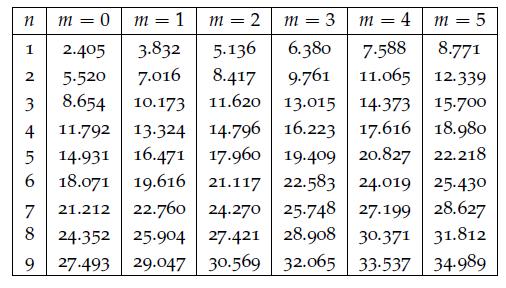

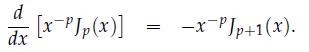
iv. Now you should have enough information to complete part d.

d. Use the results from parts b, c, and problem 16 to derive the expansion coefficients for

\[x^{2}=\sum_{j=1}^{\infty} c_{j} J_{0}\left(\alpha_{j} x\right)\]

in order to obtain the desired expansion.

Data from Table 6.3

Data from Figure 6.8

Data from Problem 18

Bessel functions \(J_{p}(\lambda x)\) are solutions of \(x^{2} y^{\prime \prime}+x y^{\prime}+\left(\lambda^{2} x^{2}-p^{2}\right) y=\) 0 . Assume that \(x \in(0,1)\) and that \(J_{p}(\lambda)=0\) and \(J_{p}(0)\) is finite.

Data from 6.60

Data from 6.61

Data from 6.63

n m=0 m 1 = m 2m 3 = == m=4m=5 1 2.405 3.832 5.136 6.380 7.588 8.771 2 5.520 7.016 8.417 9.761 11.065 12.339 3 8.654 10.173 11.620 13.015 14.373 15.700 4 11.792 13.324 14.796 16.223 17.616 18.980 5 14.931 16.471 16.471 17.960 17.960 19.409 20.827 22.218 6 18.071 19.616 21.117 22.583 24.019 25.430 7 21.212 22.760 24.270 25.748 27.199 28.627 8 24.352 25.904 27.421 28.908 30.371 31.812 9 27.493 29.047 30.569 32.065 33-537 34.989