An extended version of the Vasicek model takes the form (Hull and White, 1990) Let (t) denote

An extended version of the Vasicek model takes the form (Hull and White, 1990) 

Let λ(t) denote the time dependent market price of risk. Show that the bond price equation is given by 

Suppose we write the bond price B(r, t; T) in the form 

Show that a(t, T) and b(t, T) are governed by 

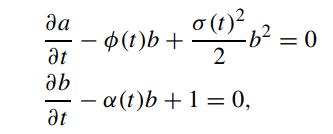
with auxiliary conditions: 

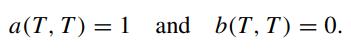
Solve for a(t, T) and b(t, T) in terms of α(t), ∅(t) and σ(t). It is desirable to express a(t, T) and b(t, T) in terms of a(0, t) and b(0, t) instead of α(t) and ∅(t). Show that the new set of governing equations for a(t, T) and b(t, T), independent of α(t) and ∅(t), are given by

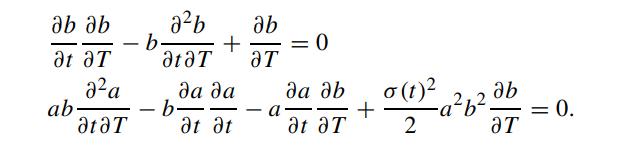
The auxiliary conditions are the known values of a(0, T) and b(0, T), a(T, T) = 1 and b(T, T) = 0. Finally, show that the solutions for b(t, T) and a(t, T), expressed in terms of b(0, T) and a(0, T), are given by 

Transcribed Image Text:

drt = [0 (t) + a(t) (d = ri)] dt + o (1) dZt.