Consider a landowner holding a piece of land who has the right to build a developed structure
Question:
Consider a landowner holding a piece of land who has the right to build a developed structure on the land or abandon the land. Let S be the value of the developed structure and H be the constant rate of holding costs (which may consist of property taxes, property maintenance costs, etc.). Assuming there is no fixed time horizon beyond which the structure cannot be developed, so the value of the land can be modeled as a perpetual American call, whose value is denoted by C(S). Let σS denote the volatility of the Brownian process followed by S and r be the riskless interest rate. Suppose the asset value of the developed structure can be hedged by other tradeable asset, use the riskless hedging principle to show that the governing equation for C(S) is given by
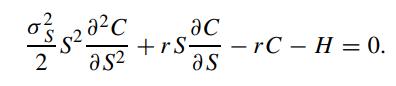 Let Z denote the lower critical value of S below which it is optimal to abandon the land. Let W be the higher critical value of S at which it is optimal to build the structure. Let X be the amount of cash investment required to build the structure. Explain why the auxiliary conditions at S = Z and S = W are prescribed by
Let Z denote the lower critical value of S below which it is optimal to abandon the land. Let W be the higher critical value of S at which it is optimal to build the structure. Let X be the amount of cash investment required to build the structure. Explain why the auxiliary conditions at S = Z and S = W are prescribed by
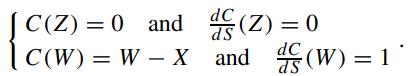
Show that the solution to the perpetual American call model is given by
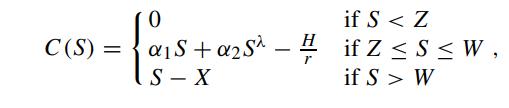
![where = - 2r H 1 w=14(x-4) a X - W H -(14)] r 1 1 - (1 - ##)(-1)/k rx (2-1)/ 2 = Z-](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1700/5/5/2/573655c5f7de7bdf1700552570968.jpg)
This pricing model has two-sided free boundaries, one is associated with the right to abandon the land and the other with the right to build the structure.
Step by Step Answer:






