Consider a three-state option model where the logarithmic return processes of the underlying assets are given by

Question:

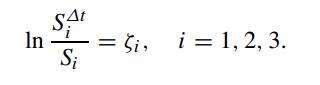
In SAt Si = $i, i = 1, 2, 3.

- Here, 5; denotes the normal random variable with mean (r At and vari- ance o At, i = 1, 2, 3. Let pij

where vi = λσi √Δt, i = 1, 2, 3. Following the Kamrad–Ritchken approach, find the probability values so that the approximating discrete distribution converges to the continuous multivariate distribution as Δt → 0. Hint: The first and last probability values are given by

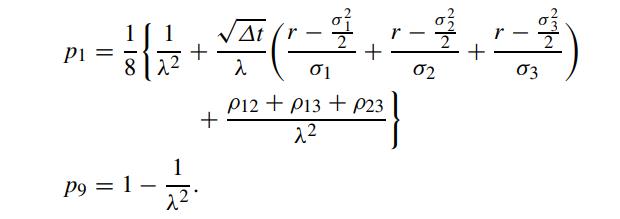
pi = + 822 pg = 1 - 1 22: + 2 + 013 + 12 A + 23 02 63