Consider the family of forward swap rates K_t[T_i,T_n],i = 0, 1, ··· ,n−1, with the common terminal payment date Tn. We would like to express the dynamics of K_t[T_i,T_n] under the terminal forward measure Q_Tn . Since Kt[T_n−1,T_n] is simply the LIBOR L_n−1(t), we have

where Z_t^Tn  is Q_Tn -Brownian. Derive the relation

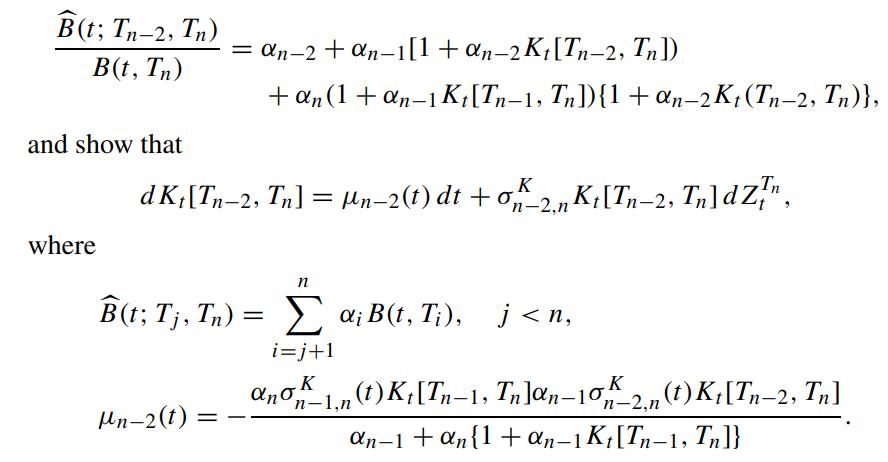
In general, deduce the relation 

and express the dynamics of K_t[T_i,T_n] under the terminal measure Q_Tn.

Transcribed Image Text:

dK:[Tn–1,Tn] dLn-1(t) Ki[Tn–1, Tn] Ln-1(t) = K = 0, -1,n(t) dz[n,