Consider the nodes in the binomial tree employed for the numerical valuation of an American put option on a nondividend paying asset. The (n,j)th node corresponds to the node which is n time steps from the current time and has j upward jumps among n moves. The put value at the (n,j)th node is denoted by Pⁿ_j . Similar to the continuous models, we define the stopping region S and continuation region C by

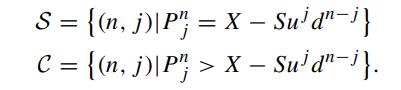 X - Sud"-i}.">That is, S (C) represents the set of nodes where the put is exercised (alive). Let N be the total number of time steps in the tree. Prove the following properties of S and C (Kim and Byun, 1994):

(i) Suppose both (n + 1,j) and (n + 1,j + 1) belong to S, then (n,j) ∈ S for 0 ≤ n ≤ N − 1, 0 ≤ j ≤ n. 

ii) Suppose (n+2,j +1) ∈ C, then (n,j) ∈ C for 0 ≤ n ≤ N−2, 0 ≤ j ≤ n. 

(iii) Suppose (n,j) ∈ S, then both (n,j − 1) and (n − 1,j − 1) ∈ S; also, suppose (n,j) ∈ C, then (n,j + 1) ∈ C and (n − 1,j) ∈ C, for 1 ≤ n ≤ N, 1 ≤ j ≤ n − 1.

Transcribed Image Text:

S = {(n, j)| P¹ = X - Su¹d"-j} C = {(n, j)|P"> X - Su¹d"-i}.