Let u and d denote the state prices corresponding to the states of asset value

Question:

Let Π_u and Π_d denote the state prices corresponding to the states of asset value going up and going down, respectively. The state prices can also be interpreted as state contingent discount rates. If no arbitrage opportunities are available, then all securities (including the bond, the asset and the call option) must have returns with the same state contingent discount rates Π_u and Π_d. Hence, the respective relations for the money market account, asset price and call option value with Π_u and Π_d are given by

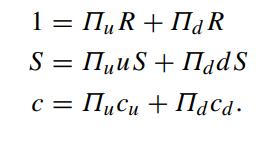
1 = uR + S = S+ dS c = + . =

By solving for Πu and Π_d from the first two equations and substituting the solutions into the third equation, show that the binomial call price formula over one period is given by

pcu + (1 - p)cd R where P = R-d u-d'