Let Y(t; ) denote the yield at time t for a discount bond with a fixed time

Let Y(t; τ) denote the yield at time t for a discount bond with a fixed time to maturity τ . The average of the constant maturity yield Y(t; τ) over a prespecified time period (0,T ] is given by

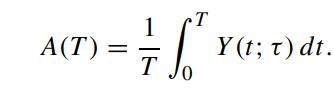
We would like to price a European call option on the average yield A(T) whose terminal payoff at time T is given by

where X is the strike price. We specify the risk neutral dynamics of the short rate process to be the continuous Ho–Lee model, where 

where f (0,t) is the initial term structure of the forward rates and Z(t) is a standard Brownian process under the risk neutral measure Q. Show that the price of the average-yield call option at time t,t

Transcribed Image Text:

A(T) = T =-=-6² Y T 0 Y(t; T) dt.