Suppose the price of a bond is dependent on the price of a commodity, denoted by Q
Question:
Suppose the price of a bond is dependent on the price of a commodity, denoted by Qt . Let the stochastic process followed by Qt be governed by
By hedging bonds of different maturities, show that the governing equation for the bond price B(Q,t) is given by [see (7.2.8)]
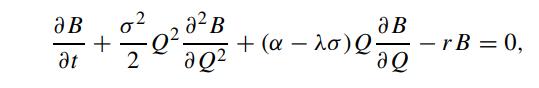
where λ is the market price of risk and r is the riskless interest rate. Since the commodity is a traded security (unlike the interest rate), the price of the commodity should also satisfy the same governing differential equation. Substituting Q for B into the differential equation, show that
Argue why the governing equation for the bond price now takes the same form as the Black–Scholes equation, which has no dependence on the risk preference.
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
The given stochastic process for the commodity price Qt is dQt a dt dZt where a is a constant is the ...View the full answer
Answered By
Larlyu mosoti
I am a professional writer willing to do several tasks free from plagiarism, grammatical errors and submit them in time. I love to do academic writing and client satisfaction is my priority. I am skilled in writing formats APA, MLA, Chicago, and Harvard I am a statistics scientist and I can help out in analyzing your data. I am okay with SPSS, EVIEWS, MS excel, and STATA data analyzing tools.
Statistical techniques: I can do linear regression, time series analysis, logistic regression, and some basic statistical calculations like probability distributions. . I'm ready for your working projects!
Services I would offer:
• Academic writing.
• Article writing.
• Data entry.
• PDF conversion.
• Word conversion
• Proofreading.
• Rewriting.
• Data analyzing.
The best reason to hire me:
- Professional and Unique work in writing.
- 100% satisfaction Guaranteed
- within required time Express delivery
- My work is plagiarism Free
- Great communication
My passion is to write vibrantly with dedication. I am loyal and confident to give my support to every client. Because Client satisfaction is much more important to me than the payment amount. A healthy client-contractor relationship benefits in the longer term. Simply inbox me if you want clean work.
3+ Reviews
10+ Question Solved
Related Book For 
Question Posted:
