Suppose we let y = ln S, the KamradRitchken trinomial scheme can be expressed as Show that
Question:
Suppose we let y = ln S, the Kamrad–Ritchken trinomial scheme can be expressed as
![]()
Show that the Taylor expansion of the above trinomial scheme is given by
![-c(y, t t) + [pic(y + v, t) + p2c(y, t) + p3(y - v, t)] e-rt = t (y,t) at 12 2 212 1-TA[(PI P30^1 (](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1700/5/5/3/881655c6499db6431700553878892.jpg)
Given the probability values stated in (6.1.19a,b,c), show that the numerical solution c(y,t) of the trinomial scheme satisfies
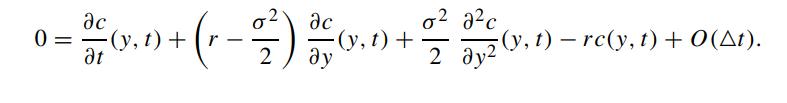
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





