Suppose we write the price function of the swaption as [see (8.4.9)], the resulting expression reveals a

Question:

Suppose we write the price function of the swaption as

n V(t; To, Tn, X) = N(d)[B(t, To) B(t, Tn)] - XN (d); B(t, T;), i=1

[see (8.4.9)], the resulting expression reveals a hedging strategy of the swaption using discount bonds with varying maturities. The replicating portfolio Π_s(t) consists of a long position in N(d₁) units of T₀-maturity bond, a short position in N(d₁) units of T_n-maturity bond and α_iN(d₂)X units of T_i-maturity bond, i = 1, 2, ··· ,n. Under the assumption of deterministic volatility function, show that the replicating portfolio Π_s(t) is self-financing.

Check whether

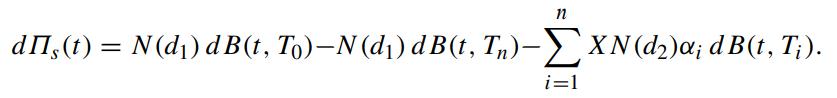
n d(t) = N(d) dB(t, To)N (d) dB(t, Tn)-XN (d); dB(t, T;). i=1